Advertisements
Advertisements
Question
Adjacent sides of a rectangle are 7 cm and 24 cm. Find the length of its diagonal.
Solution

Let `square`ABCD be the rectangle.
AB = 7 cm, BC = 24 cm
In ∆ABC,
∠B = 90° ...[Angle of a rectangle]
From Pythagoras theorem,
AC2 = AB2 + BC2
AC2 = 72 + 242
AC2 = 49 + 576
∴ AC2 = 625
∴ AC = `sqrt(625)`
∴ AC = 25 cm
APPEARS IN
RELATED QUESTIONS
ABC is a right-angled triangle and O is the mid point of the side opposite to the right angle. Explain why O is equidistant from A, B and C. (The dotted lines are drawn additionally to help you)
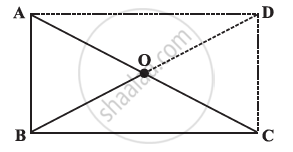
In a parallelogram ABCD, the diagonals bisect each other at O. If ∠ABC = 30°, ∠BDC = 10° and ∠CAB = 70°. Find:
∠DAB, ∠ADC, ∠BCD, ∠AOD, ∠DOC, ∠BOC, ∠AOB, ∠ACD, ∠CAB, ∠ADB, ∠ACB, ∠DBC and ∠DBA.
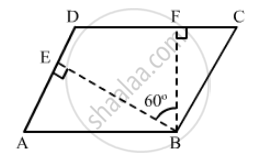
The angle between the altitudes of a parallelogram, through the same vertex of an obtuse angle of the parallelogram is 60°. Find the angles of the parallelogram.
Which of the following statement is true for a rectangle?
Its diagonals are equal.
Which of the following statement true for a square?
Its diagonals are equal to its sides.
Fill in the blank in the following, so as to make the statement true:
A rectangle is a parallelogram in which .....
Fill in the blank in the following, so as to make the statement true:
A square is a rhombus in which .....
In a rectangle ABCD, prove that ∆ACB ≅ ∆CAD.
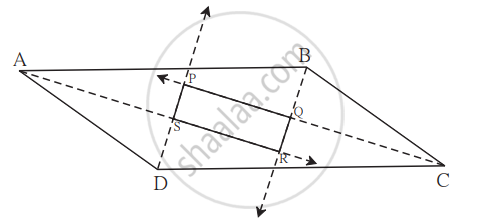
Prove that quadrilateral formed by the intersection of angle bisectors of all angles of a parallelogram is a rectangle.
State with reason whether the following statement is ‘true’ or ‘false’.
Every parallelogram is a rectangle.
