Advertisements
Advertisements
Question
An air-cored solenoid with length 30 cm, area of cross-section 25 cm2 and number of turns 500, carries a current of 2.5 A. The current is suddenly switched off in a brief time of 10−3 s. How much is the average back emf induced across the ends of the open switch in the circuit? Ignore the variation in magnetic field near the ends of the solenoid.
Solution
Length of the solenoid, l = 30 cm = 0.3 m
Area of cross-section, A = 25 cm2 = 25 × 10−4 m2
Number of turns on the solenoid, N = 500
Current in the solenoid, I = 2.5 A
Current flows for time, t = 10−3 s
Average back emf, `"e" = ("d"phi)/("dt")` .........(1)
Where,
`"d"phi` = Change in flux = NAB …........(2)
Where,
B = Magnetic field strength = `mu_0("NI")/"l"` ......(3)
Where,
`mu_0` = Permeability of free space = 4π × 10−7 T m A−1
Using equations (2) and (3) in equation (1), we get
e = `(mu_0"N"^2"IA")/("lt")`
= `(4pi xx 10^-7 xx (500)^2 xx 2.5 xx 25 xx 10^-4)/(0.3 xx 10^-3)`
= 6.5 V
Hence, the average back emf induced in the solenoid is 6.5 V.
APPEARS IN
RELATED QUESTIONS
Explain the meaning of the term mutual inductance.
Draw a necessary arrangement for winding of primary and secondary coils in a step-up transformer. State its underlying principle and derive the relation between the primary and secondary voltages in terms of number of primary and secondary turns. Mention the two basic assumptions used in obtaining the above relation.
Explain self induction and mutual induction
Consider two concentric circular coils, one of radius r1 and the other of radius r2 (r1 < r2) placed coaxially with centers coinciding with each other. Obtain the expression for the mutual inductance of the arrangement.
A coil of self-inductance 2.5H and resistance 20Ω is connected to a battery of emf 120V having the internal resistance of 5 n. Find:
1) The time constant of the circuit.
2) The current in the circuit in steady state
An emf of 96.0 mV is induced in the windings of a coil when the current in a nearby coil is increasing at the rate of 1.20 A/s. What is the mutual inductance (M) of the two coils?
A long solenoid of length l, cross-sectional area A and having N1 turns (primary coil), has a small coil of N2 turns (secondary coil) wound about its center. Determine the Mutual inductance (M) of the two coils.
The mutual inductance of two coils is 10 mH. If the current in one of the coil changes from 5 A to 1 A in 0.2 s, calculate the emf induced in the other coil. Also calculate the induced charge flowing through the coil if its resistance is 5 Ω.
Define Mutual Inductance.
Two coils P and Q have mutual inductance 'M' H. If the current in the primary is I = I0 sin `omega`t, then the maximum vlaue of e.m.f. indued in coil Q is ____________.
If number of turns in primary and secondary coils is increased to two times each, the mutual inductance ______.
Two circular coils have their centres at the same point. The mutual inductance between them will be maximum when their axes ______
Two conducting circular loops of radii R1 and R2 are placed in the same plane with their centres coinciding. If R1 >> R2, the mutual inductance M between them will be directly proportional to ______.
The mutual inductance M12 of coil 1 with respect to coil 2 ______.
- increases when they are brought nearer.
- depends on the current passing through the coils.
- increases when one of them is rotated about an axis.
- is the same as M21 of coil 2 with respect to coil 1.
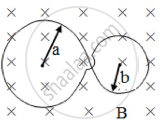
A plane loop is shaped in the form as shown in figure with radii a = 20 cm and b = 10 cm and is placed in a uniform time varying magnetic field B = B0 sin ωt, where B0 = 10 mT and ω = 100 rad/s. The amplitude of the current induced in the loop if its resistance per unit length is equal to 50 × 10-3 Ω/m. The inductance of the loop is negligible is ______ A.
The mutual inductance of a pair of adjacent coils is 1.5 H. If the current is one coil changes from 5 A to 10 A in 0.1 s, the rate of change of magnet flux linkage is ______.
