Advertisements
Advertisements
Question
Explain self induction and mutual induction
Solution
Derivation of induced e.m.f due to self induction:
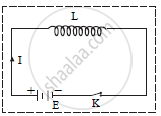
a. Consider a coil connected with battery E, plug key K and inductor L carrying current of magnitude I as shown in figure.
b. Since magnetic flux linked with the coil is directly proportional to the current.
`phi prop I`
`phi prop LI`...................(1)
where, L = constant called coefficient of self induction or self inductance of the coil, which depends upon the material of the core, number of turns, shape and area of the coil
c. Induced e.m.f in the coil is given by,
`e=-(dphi)/dt`
`e=-L(dI)/dt`.....................(2)
-ve sign in equation (ii) shows that self induced e.m.f opposes the rate of change of current.
`|e|=|-L(dI)/dt|=L(dI)/dt`
therefore Magnitude of self induced e.m.f is given by, |e|=L(dI)/dt
This is required induced e.m.f.
Derivation of induced e.m.f. due to mutual induction:
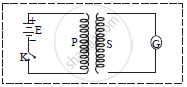
a. Consider primary coil P and secondary coil S fitted with galvanometer G are placed very close to each other as shown in figure. The coil P is connected in series with the source of e.m.f (battery) and key K.
b. When tap key K is pressed current IP passes through the coil P. Magnetic flux `phi_S` linked with secondary coil S at any instant is directly proportional to current IP through primary coil P at that instant.
`phi_s prop I_p`
`phi_s=MI_p`........................(1)
where M is constant called coefficient of mutual induction or mutual inductance of the
coil.
e.m.f induced in S at any instant is given by,` e_s=-(dphi_s)/dt`
`=-d/dt(MI_p)`
`e_s=-M(dI_p)/dt`
Magnitude of induced e.m.f is given by,
`|e_s|=-|M(dI_p)/dt|=(MdI_p)/dt`
`M=e_s/((dI_p)/dt)`
APPEARS IN
RELATED QUESTIONS
The co-efficient of mutual induction between primary and secondary coil is 2H. Calculate induced e.m.f. if current of 4A is cut off in 2.5 x 10-4 seconds
If the radius of a sphere is doubled without changing the charge on it, then electric flux originating from the sphere is ______.
Explain the meaning of the term mutual inductance.
In an experiment, two coils c1 and c2 are placed close to each other. Find out the expression for the emf induced in the coil c1 due to a change in the current through the coil c2.
The current flowing through an inductor of self inductance L is continuously increasing. Plot a graph showing the variation of Magnetic potential energy stored versus the current.
A long solenoid with 15 turns per cm has a small loop of area 2.0 cm2 placed inside the solenoid normal to its axis. If the current carried by the solenoid changes steadily from 2.0 A to 4.0 A in 0.1 s, what is the induced emf in the loop while the current is changing?
A 1.0 m long metallic rod is rotated with an angular frequency of 400 rad s−1 about an axis normal to the rod passing through its one end. The other end of the rod is in contact with a circular metallic ring. A constant and uniform magnetic field of 0.5 T parallel to the axis exists everywhere. Calculate the emf developed between the centre and the ring.
An air-cored solenoid with length 30 cm, area of cross-section 25 cm2 and number of turns 500, carries a current of 2.5 A. The current is suddenly switched off in a brief time of 10−3 s. How much is the average back emf induced across the ends of the open switch in the circuit? Ignore the variation in magnetic field near the ends of the solenoid.
Consider two concentric circular coils, one of radius r1 and the other of radius r2 (r1 < r2) placed coaxially with centers coinciding with each other. Obtain the expression for the mutual inductance of the arrangement.
A coil of self-inductance 2.5H and resistance 20Ω is connected to a battery of emf 120V having the internal resistance of 5 n. Find:
1) The time constant of the circuit.
2) The current in the circuit in steady state
Two circular loops are placed with their centres separated by a fixed distance. How would you orient the loops to have (a) the largest mutual inductance (b) the smallest mutual inductance?
Find the mutual inductance between the circular coil and the loop shown in figure.
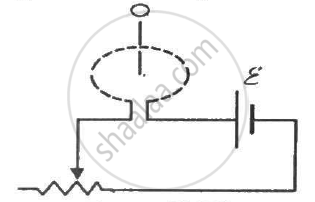
The current in a long solenoid of radius R and having n turns per unit length is given by i= i0 sin ωt. A coil having N turns is wound around it near the centre. Find (a) the induced emf in the coil and (b) the mutual inductance between the solenoid ant the coil.
A solenoid of length 20 cm, area of cross-section 4.0 cm2 and having 4000 turns is placed inside another solenoid of 2000 turns having a cross-sectional area 8.0 cm2 and length 10 cm. Find the mutual inductance between the solenoids.
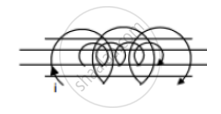
A long solenoid of length l, cross-sectional area A and having N1 turns (primary coil), has a small coil of N2 turns (secondary coil) wound about its center. Determine the Mutual inductance (M) of the two coils.
The mutual inductance of two coils is 10 mH. If the current in one of the coil changes from 5 A to 1 A in 0.2 s, calculate the emf induced in the other coil. Also calculate the induced charge flowing through the coil if its resistance is 5 Ω.
Define Mutual Inductance.
Two coils P and Q are kept near each other. When no current flows through coil P and current increases in coil Q at the rate 10 A/s, the e.m.f. in coil P is 20 mV. When coil Q carries no current and current of 1.6 A flows through coil P, the magnetic flux linked with the coil Q is ____________.
The dimensions of self or mutual inductance are given as ______.
In mutual induction, the main current remains same because ____________.
In an induction coil, the coefficient of mutual inductance is 6 henry. If a current of 10 ampere in the primary coil is cut-off in `1/1500"s"`, the e.m.f. at the terminals of the secondary coil will be ____________.
An alternating current of frequency 200 rad/s and peak value 1 A is applied to the primary of a transformer. If the coefficient of mutual induction between the primary and the secondary is 1.5H, then the voltage induced in the secondary will be approximately (π = 2217)
A coil of radius 'r' is placed on another coil (whose radius is 'R' and current flowing through it is changing) so that their centres coincide. (R>>r) if both the coils are coplanar then the mutual inductance between them is proportional to ______.
Two different wire loops are concentric and lie in the same plane. The current in the outer loop (I) is clockwise and increases with time. The induced current in the inner loop.
Alternating current of peak value `(2/pi)` ampere flows through the primary coil of transformer. The coefficient of mutual inductance between primary and secondary coil is 1 H. The peak e.m.f. induced in secondary coil is ______. (Frequency of a.c. = 50 Hz)
The mutual inductance between two coplanar concentric rings A and B of radii 'R1' and 'R2' placed in air when a current 'I' flows through ring A is (R1 >> R2) (µ0 = permeability of free space) ____________.
Two coils P and Q have mutual inductance 'M' H. If the current in the primary is I = I0 sin `omega`t, then the maximum vlaue of e.m.f. indued in coil Q is ____________.
The mutual inductance between two coils is 0.09 henry. If the current in the primary coil changes from 0 to 20 A in 0.006 s, the e.m.f. induced in the secondary coil at that instant is ____________.
The mutual inductance of a pair of coils is 0.75 H. If current in the primary coil changes from 0.5 A to zero in 0.01 s, find average induced e.m.f. in secondary coil ______.
A solenoid is connected to a battery so that a steady current flows through it. If an iron core is inserted into the solenoid, the current will ______.
If number of turns in primary and secondary coils is increased to two times each, the mutual inductance ______.
Two circular coils have their centres at the same point. The mutual inductance between them will be maximum when their axes ______
The mutual inductance M12 of coil 1 with respect to coil 2 ______.
- increases when they are brought nearer.
- depends on the current passing through the coils.
- increases when one of them is rotated about an axis.
- is the same as M21 of coil 2 with respect to coil 1.
An emf of 91 mV is induced in the windings of a coil when the current in o nearby coil is increasing at the rate of 1.3 A/s. what is the mutual inductance (M) of the two coils in mH?
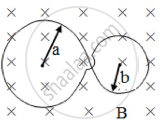
A plane loop is shaped in the form as shown in figure with radii a = 20 cm and b = 10 cm and is placed in a uniform time varying magnetic field B = B0 sin ωt, where B0 = 10 mT and ω = 100 rad/s. The amplitude of the current induced in the loop if its resistance per unit length is equal to 50 × 10-3 Ω/m. The inductance of the loop is negligible is ______ A.
Two circular loops, one of small radius r and the other of larger radius R, such that R >> r, are placed coaxially with centres coinciding. Obtain the mutual inductance of the arrangement.
Write the S.I. unit of mutual inductance.
The mutual inductance of a pair of adjacent coils is 1.5 H. If the current is one coil changes from 5 A to 10 A in 0.1 s, the rate of change of magnet flux linkage is ______.
A rectangular coil of wire 50 turn each of area 6 x 10-4 m2 is freely suspended in a field of 3 x 10-2 Wb / m2. Calculate the current flowing through the coil when it deflects through 60°, when torsional constant is 3.82 x 10-6 SI unit.
State and define the SI unit of mutual inductance.
Two coils having self inductances L1 = 75 mH and L2 = 55 mH are coupled with each other. The coefficient of coupling (K) is 0. 75. Calculate the mutual inductance (M) of the two coils
