Advertisements
Advertisements
Question
An area is paved with square tiles of a certain size and the number required is 128. If the tiles had been 2 cm smaller each way, 200 tiles would have been needed to pave the same area. Find the size of the larger tiles.
Solution
Let the size of the larger tiles be x cm.
Area of larger tiles = x2 cm2
Number of larger tiles required to pave an area is 128.
So, the area needed to be paved = 128x2 cm2 ...(1)
Size of smaller tiles = (x – 2) cm
Area of smaller tiles = (x – 2)2 cm2
Number of larger tiles required to pave an area is 200.
So, the area needed to be paved = 200(x – 2)2 cm2 ...(2)
Therefore, from (1) and (2), we have:
128x2 = 200(x – 2)2
128x2 = 200x2 + 800 – 800x
72x2 – 800x + 800 = 0
9x2 – 100x + 100 = 0
9x2 – 90x – 10x + 100 = 0
9x(x – 10) – 10(x – 10) = 0
(x – 10)(9x – 10) = 0
`x = 10,10/9`
If `x = 10/9`,
Then `x - 2 = 10/9 - 2`
= `(10 - 18)/9`
= `(-8)/9`
Which is not possible.
Hence, the size of the larger tiles is 10 cm.
APPEARS IN
RELATED QUESTIONS
The perimeter of a rectangle is 104 m and its area is 640 m2. Find its length and breadth.
A footpath of uniform width runs round the inside of a rectangular field 32 m long and 24 m wide. If the path occupies 208 m2, find the width of the footpath.
Two squares have sides x cm and (x + 4) cm. The sum of their area is 656 sq. cm. Express this as an algebraic equation in x and solve the equation to find the sides of the squares.
The dimensions of a rectangular field are 50 m and 40 m. A flower bed is prepared inside this field leaving a gravel path of uniform width all around the flower bed. The total cost of laying the flower bed and gravelling the path at Rs. 30 and Rs. 20 per square metre, respectively, is Rs. 52,000. Find the width of the gravel path.
A square lawn is bounded on three sides by a path 4 m wide. If the area of the path is `7/8` that of the lawn, find the dimensions of the lawn.
A car made a run of 390 km in ‘x’ hours. If the speed had been 4 km/hour more, it would have taken 2 hours less for the journey. Find ‘x’.
The perimeter of a rectangular field is 28 m and its area is 40 sq. m. Its sides are ______.
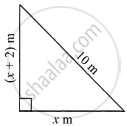
In the given figure, the value of x is ______.
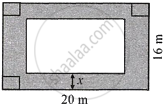
If the width of the uniform shaded portion of x m; its area in terms of x is ______.
The length of a rectangle is 3 m more than its width. If its area is 180 m2; the length of the rectangle is ______.
