Advertisements
Advertisements
Question
An electric heater supplies heat to a system at a rate of 100W. If the system performs work at a rate of 75 Joules per second. At what rate is the internal energy increasing?
Solution 1
Heat is supplied to the system at a rate of 100 W.
∴Heat supplied, Q = 100 J/s
The system performs at a rate of 75 J/s.
∴Work done, W = 75 J/s
From the first law of thermodynamics, we have:
Q = U + W
Where,
U = Internal energy
∴U = Q – W
= 100 – 75
= 25 J/s
= 25 W
Therefore, the internal energy of the given electric heater increases at a rate of 25 W.
Solution 2
Here `triangle Q = 100 W = 100 "J/s"`
`triangle W = 75"J/s"`
Since `triangle Q = triangle uu + triangle W`
= 100 - 75 = 25 J/s
APPEARS IN
RELATED QUESTIONS
For an Isochoric process
A cycle followed by an engine (made of one mole of perfect gas in a cylinder with a piston) is shown in figure.
A to B : volume constant
B to C : adiabatic
C to D : volume constant
D to A : adiabatic
VC = VD = 2VA = 2VB
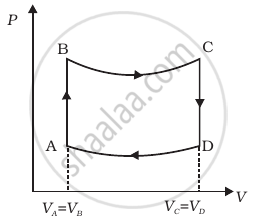
- In which part of the cycle heat is supplied to the engine from outside?
- In which part of the cycle heat is being given to the surrounding by the engine?
- What is the work done by the engine in one cycle? Write your answer in term of PA, PB, VA.
- What is the efficiency of the engine?
(γ = `5/3` for the gas), (Cv = `3/2` R for one mole)
A cycle followed by an engine (made of one mole of an ideal gas in a cylinder with a piston) is shown in figure. Find heat exchanged by the engine, with the surroundings for each section of the cycle. (Cv = (3/2)R)
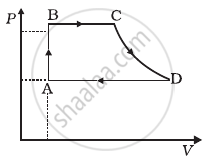
- AB : constant volume
- BC : constant pressure
- CD : adiabatic
- DA : constant pressure
The first law of thermodynamics is concerned with the conservation of ______.
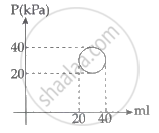
In the reported figure, heat energy absorbed by a system in going through a cyclic process is ______ πJ.
An electric appliance supplies 6000 J/min heat to the system. If the system delivers a power of 90 W. How long it would take to increase the internal energy by 2.5 × 103 J?
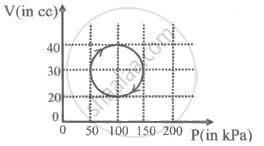
A system is taken through a cyclic process represented by a circle as shown. The heat absorbed by the system is ______.
One mole of an ideal gas is allowed to expand reversibly and adiabatically from a temperature of 27°C. If the work done during the process is 3 kJ, the final temperature will be equal to ______.
(Cv = 20 JK−1)
A soap bubble in vacuum has a radius of 3 cm and another soap bubble in vacuum has a radius of 4 cm. If the two bubbles coalesce under isothermal condition, then the radius of the new bubble is ______.
One mole of an ideal gas is initially kept in a cylinder with a movable frictionless and massless piston at pressure of 1.01MPa, and temperature 27°C. It is then expanded till its volume is doubled. How much work is done if the expansion is isobaric?
