Advertisements
Advertisements
Question
A cycle followed by an engine (made of one mole of an ideal gas in a cylinder with a piston) is shown in figure. Find heat exchanged by the engine, with the surroundings for each section of the cycle. (Cv = (3/2)R)
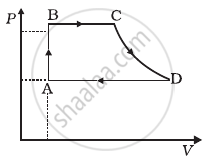
- AB : constant volume
- BC : constant pressure
- CD : adiabatic
- DA : constant pressure
Solution
a. By using the first law of thermodynamics, we can find the amount of heat associated with each process
For process AB
Volume is constant, hence work done dW = 0
According to first law of thermodynamics,
`ΔQ = ΔU + ΔW = ΔU + 0 = ΔU`
= `nCvΔT = nCv(T_B - T_A)`
= `3/2 R(T_B - T_A)` .....(∵ n = 1)
= `3/2 (RT_B - RT_A)`
= `3/2 (P_AV_B - P-AV_A)`
= `3/2 (P_B - P_A)V_A` .....[∵ VB = VA]
b. For process BC, P = constant
`ΔQ = ΔU + ΔW`
= `3/2 R(T_C - T_B) + P_B(V_C - V_B)`
= `3/2 (P_CV_C - P+BV_B) + P_B (V_C - V_B)`
= `5/2 P_B (V_C - V_B)`
Heat exchanged = `5/2 P_B (V_C - V_A)` .....(∵ PB = PC and PB = VA)
c. For process CD, QCD = 0 .....(As the change is adiabatic.)
d. In process DA involves compression of gas from VD to VA at constant pressure PA.
∴ Heat exchanged can be calculated in a similar way as process BC.
Hence, `ΔQ = 5/2 P_A(V_A - V_D)`.
APPEARS IN
RELATED QUESTIONS
The internal energy of an ideal gas decreases by the same amount as the work done by the system.
(a) The process must be adiabatic.
b) The process must be isothermal.
(c) The process must be isobaric.
(d) The temperature must decrease.
Calculate the change in internal energy of a gas kept in a rigid container when 100 J of heat is supplied to it.
Choose the correct option.
Which of the following is an example of the first law of thermodynamics?
For an Isothermal process
Which of the following are TRUE for a reversible isothermal process?
(i) ∆U = 0
(ii) ∆H = 0
(iii) Q = W
(iv) ∆T = 0
"The mass and energy both are conserved in an isolated system", is the statement of ______.
Consider two containers A and B containing identical gases at the same pressure, volume and temperature. The gas in container A is compressed to half of its original volume isothermally while the gas in container B is compressed to half of its original value adiabatically. The ratio of final pressure of gas in B to that of gas in A is ______.
In an adiabatic expansion of 2 moles of a gas, the initial pressure was 1.013 × 105 Pa, the initial volume was 22.4 L, the final pressure was 3.191 × 104 Pa and the final volume was 44.8 L. Find the work done by the gas on its surroundings. Taken `γ = 5/3`.
A monoatomic gas at 27°C is adiabatically compressed to 80% of its initial volume. Find the final temperature of the gas.
Define the isothermal process.
