Advertisements
Advertisements
Question
Consider that an ideal gas (n moles) is expanding in a process given by P = f(V), which passes through a point (V0, P0). Show that the gas is absorbing heat at (P0, V0) if the slope of the curve P = f(V) is larger than the slope of the adiabat passing through (P0, V0).
Solution
Slope of the graph at `(V_0, P_0) = ((dP)/(dV))_((V_0, P_0)`
We know that for the adiabatic process `PV^γ = K`
⇒ `P = K/V^γ`
⇒ `(dP)/(dV) = K(-γ) V^(-γ-1)`
⇒ `(dP)/(dV) = - γPV^γ V^-γ V^-1`
⇒`(dP)/(dV) = (-γP)/V`
⇒ `((dP)/(dV))_((V_0"," P_0)) = (-γP_0)/V_0`
Now, heat absorbed in the process `P = f(V)`,
∴ `dQ = dU + dW`
⇒ `dQ = nC_VdT + PdV` ......(i)
We know that `PV = nRT`. Therefore, we get
⇒ `T = (PV)/(nR)`
⇒ `T = V/(nR) f(V)` .....(Given, `P = f(V)`)
⇒ `(dT)/(dV) = 1/(nR)` .....`[f(V) + Vf^' (V)]`
Now, continue solving equation (i)
⇒ `(dQ)/(dV) = nCv (dT)/(dV) + P(dV)/(dV)`
⇒ `(dQ)/(dV) = (nCv)/(nR) [f(V) + Vf^' (V)] + P`
⇒ `((dQ)/(dV))_(V = V_0) = (Cv)/R [f(V_0) + V_0f^' (V_0)] + f(V_0)`
⇒ `((dQ)/(dV))_(V = V_0) = f(V_0) [(Cv)/R + 1] + V_0f^' (V_0) (Cv)/R`
We know that `C_P - C_V = R`
⇒ `(C_P)/(C_V) - 1 = R/(C_V)`
⇒ `γ - 1 = R/(C_V)`
⇒ `C_V = R/(γ - 1)`
⇒ `C_V/R = 1/(γ - 1)`
⇒ `((dQ)/(dV))_(V = V_0) = f(V_0) [1/(γ - 1) + 1] + V_0f^' (V_0) 1/(γ - 1)`
⇒ `((dQ)/(dV))_(V = V_0) = f(V_0) [(1 + γ - 1)/(γ - 1)] + (V_0f^' (V_0))/(γ - 1)`
⇒ `((dQ)/(dV))_(V = V_0) = γ/((γ - 1)) f(V_0) + V_0 (f^' (V_0))/(γ - 1)`
⇒ `((dQ)/(dV))_(V = V_0) = 1/((γ - 1)) [γf (V_0) + V_0f^' (V_0)]`
⇒ `((dQ)/(dV))_(V = V_0) = 1/((γ - 1)) [γP_0 + V_0f^' (V_0)]` .....`(∵ f(V_0) = P_0)`
If γ > 1, so `(1/(γ - 1))` is positive.
Then, heat is absorbed where `((dQ)/(dV))_(V = V_0) > 0` when gas expands.
Hence, `γP_0 + V_0f^' (V_0) > 0`
⇒ `V_0f^' (V_0) > (- γ P_0)`
⇒ `f^' (V_0) > ((- γP_0)/V_0)`
APPEARS IN
RELATED QUESTIONS
Write the mathematical expression of the First Law of Thermodynamics for Isothermal Process
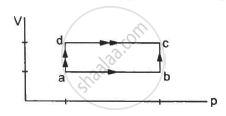
When a system is taken through the process abc shown in figure, 80 J of heat is absorbed by the system and 30 J of work is done by it. If the system does 10 J of work during the process adc, how much heat flows into it during the process?
For an Isochoric process
In a given process for an ideal gas, dW = 0 and dQ < 0. Then for the gas ____________.
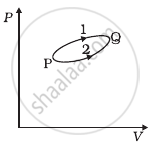
A system goes from P to Q by two different paths in the P-V diagram as shown in figure. Heat given to the system in path 1 is 1000 J. The work done by the system along path 1 is more than path 2 by 100 J. What is the heat exchanged by the system in path 2?
Consider a cycle tyre being filled with air by a pump. Let V be the volume of the tyre (fixed) and at each stroke of the pump ∆V(V) of air is transferred to the tube adiabatically. What is the work done when the pressure in the tube is increased from P1 to P2?
Write the mathematical equation for the first law of thermodynamics for:
Isothermal process
In an adiabatic expansion of 2 moles of a gas, the initial pressure was 1.013 × 105 Pa, the initial volume was 22.4 L, the final pressure was 3.191 × 104 Pa and the final volume was 44.8 L. Find the work done by the gas on its surroundings. Taken `γ = 5/3`.
Choose the correct relation with reason.
Obtain an expression for the workdone by a gas in an isothermal process.
