Advertisements
Advertisements
प्रश्न
Consider that an ideal gas (n moles) is expanding in a process given by P = f(V), which passes through a point (V0, P0). Show that the gas is absorbing heat at (P0, V0) if the slope of the curve P = f(V) is larger than the slope of the adiabat passing through (P0, V0).
उत्तर
Slope of the graph at `(V_0, P_0) = ((dP)/(dV))_((V_0, P_0)`
We know that for the adiabatic process `PV^γ = K`
⇒ `P = K/V^γ`
⇒ `(dP)/(dV) = K(-γ) V^(-γ-1)`
⇒ `(dP)/(dV) = - γPV^γ V^-γ V^-1`
⇒`(dP)/(dV) = (-γP)/V`
⇒ `((dP)/(dV))_((V_0"," P_0)) = (-γP_0)/V_0`
Now, heat absorbed in the process `P = f(V)`,
∴ `dQ = dU + dW`
⇒ `dQ = nC_VdT + PdV` ......(i)
We know that `PV = nRT`. Therefore, we get
⇒ `T = (PV)/(nR)`
⇒ `T = V/(nR) f(V)` .....(Given, `P = f(V)`)
⇒ `(dT)/(dV) = 1/(nR)` .....`[f(V) + Vf^' (V)]`
Now, continue solving equation (i)
⇒ `(dQ)/(dV) = nCv (dT)/(dV) + P(dV)/(dV)`
⇒ `(dQ)/(dV) = (nCv)/(nR) [f(V) + Vf^' (V)] + P`
⇒ `((dQ)/(dV))_(V = V_0) = (Cv)/R [f(V_0) + V_0f^' (V_0)] + f(V_0)`
⇒ `((dQ)/(dV))_(V = V_0) = f(V_0) [(Cv)/R + 1] + V_0f^' (V_0) (Cv)/R`
We know that `C_P - C_V = R`
⇒ `(C_P)/(C_V) - 1 = R/(C_V)`
⇒ `γ - 1 = R/(C_V)`
⇒ `C_V = R/(γ - 1)`
⇒ `C_V/R = 1/(γ - 1)`
⇒ `((dQ)/(dV))_(V = V_0) = f(V_0) [1/(γ - 1) + 1] + V_0f^' (V_0) 1/(γ - 1)`
⇒ `((dQ)/(dV))_(V = V_0) = f(V_0) [(1 + γ - 1)/(γ - 1)] + (V_0f^' (V_0))/(γ - 1)`
⇒ `((dQ)/(dV))_(V = V_0) = γ/((γ - 1)) f(V_0) + V_0 (f^' (V_0))/(γ - 1)`
⇒ `((dQ)/(dV))_(V = V_0) = 1/((γ - 1)) [γf (V_0) + V_0f^' (V_0)]`
⇒ `((dQ)/(dV))_(V = V_0) = 1/((γ - 1)) [γP_0 + V_0f^' (V_0)]` .....`(∵ f(V_0) = P_0)`
If γ > 1, so `(1/(γ - 1))` is positive.
Then, heat is absorbed where `((dQ)/(dV))_(V = V_0) > 0` when gas expands.
Hence, `γP_0 + V_0f^' (V_0) > 0`
⇒ `V_0f^' (V_0) > (- γ P_0)`
⇒ `f^' (V_0) > ((- γP_0)/V_0)`
APPEARS IN
संबंधित प्रश्न
Write the mathematical expression of the First Law of Thermodynamics for Isothermal Process
When we heat an object, it expands. Is work done by the object in this process? Is heat given to the object equal to the increase in its internal energy?
Calculate the change in internal energy of a gas kept in a rigid container when 100 J of heat is supplied to it.
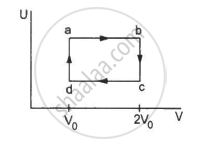
Figure shows the variation in the internal energy U with the volume V of 2.0 mol of an ideal gas in a cyclic process abcda. The temperatures of the gas at b and c are 500 K and 300 K respectively. Calculate the heat absorbed by the gas during the process.
The process, in which no heat enters or leaves the system, is termed as ____________.
For a particular reaction, the system absorbs 8 kJ of heat and does 2.5 kJ of work on its surrounding. What will be the change in internal energy of the system?
Which among the following equations represents the first law of thermodynamics under isobaric conditions?
A soap bubble in vacuum has a radius of 3 cm and another soap bubble in vacuum has a radius of 4 cm. If the two bubbles coalesce under isothermal condition, then the radius of the new bubble is ______.
What is Isobaric process?
Explain the formulation of first law of thrmodynamics.
