Advertisements
Advertisements
प्रश्न
Consider that an ideal gas (n moles) is expanding in a process given by P = f(V), which passes through a point (V0, P0). Show that the gas is absorbing heat at (P0, V0) if the slope of the curve P = f(V) is larger than the slope of the adiabat passing through (P0, V0).
उत्तर
Slope of the graph at `(V_0, P_0) = ((dP)/(dV))_((V_0, P_0)`
We know that for the adiabatic process `PV^γ = K`
⇒ `P = K/V^γ`
⇒ `(dP)/(dV) = K(-γ) V^(-γ-1)`
⇒ `(dP)/(dV) = - γPV^γ V^-γ V^-1`
⇒`(dP)/(dV) = (-γP)/V`
⇒ `((dP)/(dV))_((V_0"," P_0)) = (-γP_0)/V_0`
Now, heat absorbed in the process `P = f(V)`,
∴ `dQ = dU + dW`
⇒ `dQ = nC_VdT + PdV` ......(i)
We know that `PV = nRT`. Therefore, we get
⇒ `T = (PV)/(nR)`
⇒ `T = V/(nR) f(V)` .....(Given, `P = f(V)`)
⇒ `(dT)/(dV) = 1/(nR)` .....`[f(V) + Vf^' (V)]`
Now, continue solving equation (i)
⇒ `(dQ)/(dV) = nCv (dT)/(dV) + P(dV)/(dV)`
⇒ `(dQ)/(dV) = (nCv)/(nR) [f(V) + Vf^' (V)] + P`
⇒ `((dQ)/(dV))_(V = V_0) = (Cv)/R [f(V_0) + V_0f^' (V_0)] + f(V_0)`
⇒ `((dQ)/(dV))_(V = V_0) = f(V_0) [(Cv)/R + 1] + V_0f^' (V_0) (Cv)/R`
We know that `C_P - C_V = R`
⇒ `(C_P)/(C_V) - 1 = R/(C_V)`
⇒ `γ - 1 = R/(C_V)`
⇒ `C_V = R/(γ - 1)`
⇒ `C_V/R = 1/(γ - 1)`
⇒ `((dQ)/(dV))_(V = V_0) = f(V_0) [1/(γ - 1) + 1] + V_0f^' (V_0) 1/(γ - 1)`
⇒ `((dQ)/(dV))_(V = V_0) = f(V_0) [(1 + γ - 1)/(γ - 1)] + (V_0f^' (V_0))/(γ - 1)`
⇒ `((dQ)/(dV))_(V = V_0) = γ/((γ - 1)) f(V_0) + V_0 (f^' (V_0))/(γ - 1)`
⇒ `((dQ)/(dV))_(V = V_0) = 1/((γ - 1)) [γf (V_0) + V_0f^' (V_0)]`
⇒ `((dQ)/(dV))_(V = V_0) = 1/((γ - 1)) [γP_0 + V_0f^' (V_0)]` .....`(∵ f(V_0) = P_0)`
If γ > 1, so `(1/(γ - 1))` is positive.
Then, heat is absorbed where `((dQ)/(dV))_(V = V_0) > 0` when gas expands.
Hence, `γP_0 + V_0f^' (V_0) > 0`
⇒ `V_0f^' (V_0) > (- γ P_0)`
⇒ `f^' (V_0) > ((- γP_0)/V_0)`
APPEARS IN
संबंधित प्रश्न
The pressure of a gas changes linearly with volume from 10 kPa, 200 cc to 50 kPa, 50 cc. (a) Calculate the work done by the gas. (b) If no heat is supplied or extracted from the gas, what is the change in the internal energy of the gas?
When a system is taken through the process abc shown in figure, 80 J of heat is absorbed by the system and 30 J of work is done by it. If the system does 10 J of work during the process adc, how much heat flows into it during the process?
The compressibility of water is 5 × 10-10 m2/N. Pressure of 15 × 106 Pa is applied on 100 ml volume of water. The change in the volume of water is ______.
Two moles of an ideal gas is expanded isothermally and reversibly at 300 K from 1 L to 10 L. The enthalpy change in kJ is ______.
For a particular reaction, the system absorbs 8 kJ of heat and does 2.5 kJ of work on its surrounding. What will be the change in internal energy of the system?
Three copper blocks of masses M1, M2 and M3 kg respectively are brought into thermal contact till they reach equilibrium. Before contact, they were at T1, T2, T3 (T1 > T2 > T3). Assuming there is no heat loss to the surroundings, the equilibrium temprature T is (s is specific heat of copper)
Consider a P-V diagram in which the path followed by one mole of perfect gas in a cylindrical container is shown in figure.
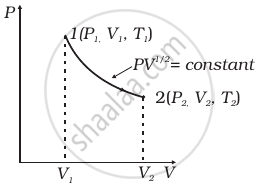
- Find the work done when the gas is taken from state 1 to state 2.
- What is the ratio of temperature T1/T2, if V2 = 2V1?
- Given the internal energy for one mole of gas at temperature T is (3/2) RT, find the heat supplied to the gas when it is taken from state 1 to 2, with V2 = 2V1.
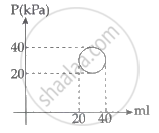
In the reported figure, heat energy absorbed by a system in going through a cyclic process is ______ πJ.
Explain the formulation of first law of thrmodynamics.
Define the isothermal process.
