Advertisements
Advertisements
Question
Consider one mole of perfect gas in a cylinder of unit cross section with a piston attached (figure). A spring (spring constant k) is attached (unstretched length L) to the piston and to the bottom of the cylinder. Initially the spring is unstretched and the gas is in equilibrium. A certain amount of heat Q is supplied to the gas causing an increase of volume from V0 to V1.
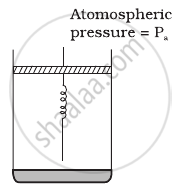
- What is the initial pressure of the system?
- What is the final pressure of the system?
- Using the first law of thermodynamics, write down a relation between Q, Pa, V, Vo and k.
Solution
a. Initially the piston is in equilibrium hence, Pf = Pa
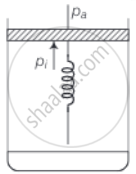
b. On supplying heat, the gas expands from V0 to V1
∴ Increase in volume of the gas = V1 – V0
As the piston is of the unit cross-sectional area hence, extension in the spring
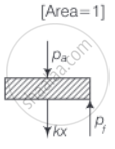
`x = (V_1 - V_0)/"Area" = V_1 - V_0`
∴ Force exerted by the spring on the piston
= `F = kx = k(V_1 - V_0)`
Hence, Final pressure = `P_f = P_a + kx`
= `P_a + k xx (V_1 - V_0)`
c. From the first law of thermodynamics `dQ = du + dW`
If T is the final temperature of the gas. then increases in internal energy
`dU = C_v (T - T_0) = C_v (T - T_0)`
We can write, `T = (P_f V_1)/R - [(P_a + k(V_1 - V_0))/R] V_1/R`
Work done by the gas = PdV + increase in PE of the spring
= `P_a (V_1 - V_0) + 1/2 kx^2`
Now, we can write `dQ = dU + dW`
= `C_V (T - T_0) + P_a (V - V_0) + 1/2 kx^2`
= `C_V (T - T_0) + P_a (V_ V_0) + 1/2 (V_1 - V_0)^2`
This is the required relation.
APPEARS IN
RELATED QUESTIONS
10 kg of four different gases (Cl2, CH4, O2, N2) expand isothermally and reversibly from 20 atm to 10 atm. The order of amount of work will be ____________.
When heat energy of 2000 joules is supplied to a gas at constant pressure 2.1 x 105 N/m2, there is an increase in its volume equal to 2.5 x 10-3 m3. The increase in internal energy of the gas in joules is ____________.
Consider a cycle followed by an engine (Figure)
1 to 2 is isothermal
2 to 3 is adiabatic
3 to 1 is adiabatic
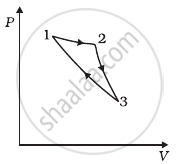
Such a process does not exist because ______.
- heat is completely converted to mechanical energy in such a process, which is not possible.
- mechanical energy is completely converted to heat in this process, which is not possible.
- curves representing two adiabatic processes don’t intersect.
- curves representing an adiabatic process and an isothermal process don’t intersect.
Consider a cycle tyre being filled with air by a pump. Let V be the volume of the tyre (fixed) and at each stroke of the pump ∆V(V) of air is transferred to the tube adiabatically. What is the work done when the pressure in the tube is increased from P1 to P2?
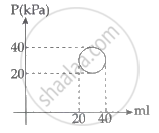
In the reported figure, heat energy absorbed by a system in going through a cyclic process is ______ πJ.
An insulated container of gas has two chambers separated by an insulating partition. One of the chambers has volume V1 and contains ideal gas at pressure P1 and temperature T1. The other chamber has volume V2 and contains ideal gas at pressure P2 and temperature T2. If the partition is removed without doing any work on the gas, the final equilibrium temperature of the gas in the container will be ______.
Which among the following equations represents the first law of thermodynamics under isobaric conditions?
The amount of work done in increasing the voltage across the plates of capacitor from 5 V to 10 V is W. The work done in increasing it from 10 V to 15 V will be ______.
In an adiabatic expansion of 2 moles of a gas, the initial pressure was 1.013 × 105 Pa, the initial volume was 22.4 L, the final pressure was 3.191 × 104 Pa and the final volume was 44.8 L. Find the work done by the gas on its surroundings. Taken `γ = 5/3`.
Define isochoric process
