Advertisements
Advertisements
Question
Obtain an expression for the workdone by a gas in an isothermal process.
Solution 1
Work done by a gas in an isothermal process:
Consider the moles of a gas contained within a cylinder with a moveable, light, and frictionless piston. Let Pi, Vi, and T represent the gas's initial pressure, volume, and absolute temperature, respectively.
Consider an isothermal expansion (or compression) of a gas, where Pf, vf, and T are the final pressure, volume, and absolute temperature of the gas, respectively.
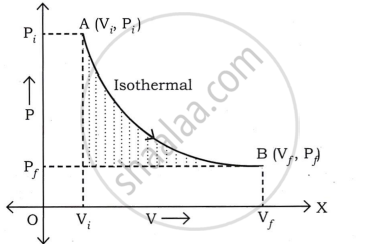
For an isothermal change,
PiVi = PfVf = constant
If the gas behaves like an ideal gas, its equation of state is
PV = nRT = constant ...(i) ....(as T = constant, R is universal gas constant)
The work done in a minuscule isothermal expansion is given by
dW = PdV ...(ii)
The total work done in completing the expansion from initial volume vi to final volume Vf is denoted by
`W = int_(v_i)^(v_f) PdV`
∴ `W = nRT int_(v_i)^(v_f) (dV)/V` ...[from(i)]
∴ W = nRT [In Vf - InVi]
∴ W = nRT In `V_f/V_i`
∴ W = 2.303 nRT `log_10 V_f/V_i`
Solution 2
Consider the isothermal expansion of an ideal gas. During this process, small work is done, and it is given by
dW = PdV
We get the total work done by integrating the above equation with the limit Vi to Vf.
`W = int_(V_i)^(V_f)Pdv` ...(i)
But we know that for an ideal gas, PV = nRT.
∴ Equation (i) becomes,
`W = int_(V_i)^(V_f)(nRT)/V dV`
`W = nRT int_(V_i)^(V_f)(dV)/V`
`W = nRT [log V]_(V_i)^(V_f)`
`W = nRT log_e (V_f/V_i)`
or `W = 2.303 nRT log_10 (V_f/V_i)`
APPEARS IN
RELATED QUESTIONS
The first law of thermodynamics is a statement of ____________ .
The pressure of a gas changes linearly with volume from 10 kPa, 200 cc to 50 kPa, 50 cc. (a) Calculate the work done by the gas. (b) If no heat is supplied or extracted from the gas, what is the change in the internal energy of the gas?
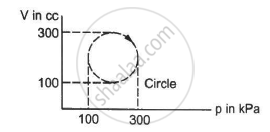
Calculate the heat absorbed by a system in going through the cyclic process shown in figure.
Find the change in the internal energy of 2 kg of water as it is heated from 0°C to 4°C. The specific heat capacity of water is 4200 J kg−1 K−1 and its densities at 0°C and 4°C are 999.9 kg m−3 and 1000 kg m−3 respectively. Atmospheric pressure = 105 Pa.
An adiabatic vessel of total volume V is divided into two equal parts by a conducting separator. The separator is fixed in this position. The part on the left contains one mole of an ideal gas (U = 1.5 nRT) and the part on the right contains two moles of the same gas. Initially, the pressure on each side is p. The system is left for sufficient time so that a steady state is reached. Find (a) the work done by the gas in the left part during the process, (b) the temperature on the two sides in the beginning, (c) the final common temperature reached by the gases, (d) the heat given to the gas in the right part and (e) the increase in the internal energy of the gas in the left part.
Answer the following in one or two sentences.
State the first law of thermodynamics.
For an Isothermal process
10 kg of four different gases (Cl2, CH4, O2, N2) expand isothermally and reversibly from 20 atm to 10 atm. The order of amount of work will be ____________.
A sample of gas absorbs 4000 kJ of heat and surrounding does 2000 J of work on sample. What is the value of ∆U?
The compressibility of water is 5 × 10-10 m2/N. Pressure of 15 × 106 Pa is applied on 100 ml volume of water. The change in the volume of water is ______.
When heat energy of 2000 joules is supplied to a gas at constant pressure 2.1 x 105 N/m2, there is an increase in its volume equal to 2.5 x 10-3 m3. The increase in internal energy of the gas in joules is ____________.
120 J of heat is added to a gaseous system, whose internal energy change is 60 J, then the amount of external work done is ____________.
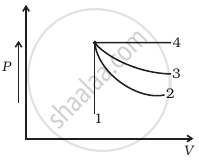
An ideal gas undergoes four different processes from the same initial state (figure). Four processes are adiabatic, isothermal, isobaric and isochoric. Out of 1, 2, 3 and 4 which one is adiabatic.
If an average person jogs, hse produces 14.5 × 103 cal/min. This is removed by the evaporation of sweat. The amount of sweat evaporated per minute (assuming 1 kg requires 580 × 103 cal for evaparation) is ______.
An ideal gas undergoes cyclic process ABCDA as shown in given P-V diagram (figure). The amount of work done by the gas is ______.

Three copper blocks of masses M1, M2 and M3 kg respectively are brought into thermal contact till they reach equilibrium. Before contact, they were at T1, T2, T3 (T1 > T2 > T3). Assuming there is no heat loss to the surroundings, the equilibrium temprature T is (s is specific heat of copper)
Air pressure in a car tyre increases during driving. Explain.
A cycle followed by an engine (made of one mole of perfect gas in a cylinder with a piston) is shown in figure.
A to B : volume constant
B to C : adiabatic
C to D : volume constant
D to A : adiabatic
VC = VD = 2VA = 2VB
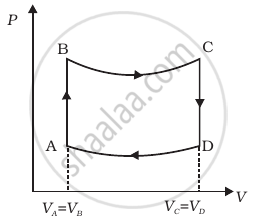
- In which part of the cycle heat is supplied to the engine from outside?
- In which part of the cycle heat is being given to the surrounding by the engine?
- What is the work done by the engine in one cycle? Write your answer in term of PA, PB, VA.
- What is the efficiency of the engine?
(γ = `5/3` for the gas), (Cv = `3/2` R for one mole)
An electric appliance supplies 6000 J/min heat to the system. If the system delivers a power of 90 W. How long it would take to increase the internal energy by 2.5 × 103 J?
An insulated container of gas has two chambers separated by an insulating partition. One of the chambers has volume V1 and contains ideal gas at pressure P1 and temperature T1. The other chamber has volume V2 and contains ideal gas at pressure P2 and temperature T2. If the partition is removed without doing any work on the gas, the final equilibrium temperature of the gas in the container will be ______.
Which among the following equations represents the first law of thermodynamics under isobaric conditions?
The amount of work done in increasing the voltage across the plates of capacitor from 5 V to 10 V is W. The work done in increasing it from 10 V to 15 V will be ______.
An ideal gas (γ = 1.5) is expanded adiabatically. How many times has the gas had to be expanded to reduce the root mean square velocity of molecules two times?
If the adiabatic ratio for a gas is 5/3, find the molar specific heat capacity of the gas at (i) constant volume (ii) constant pressure.
What is Isobaric process?
A monoatomic gas at 27°C is adiabatically compressed to 80% of its initial volume. Find the final temperature of the gas.
Choose the correct relation with reason.
