Advertisements
Advertisements
प्रश्न
Obtain an expression for the workdone by a gas in an isothermal process.
उत्तर १
Work done by a gas in an isothermal process:
Consider the moles of a gas contained within a cylinder with a moveable, light, and frictionless piston. Let Pi, Vi, and T represent the gas's initial pressure, volume, and absolute temperature, respectively.
Consider an isothermal expansion (or compression) of a gas, where Pf, vf, and T are the final pressure, volume, and absolute temperature of the gas, respectively.
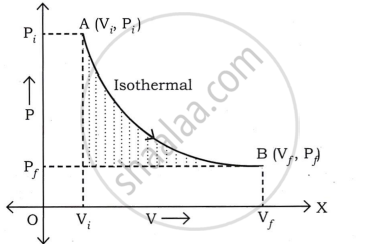
For an isothermal change,
PiVi = PfVf = constant
If the gas behaves like an ideal gas, its equation of state is
PV = nRT = constant ...(i) ....(as T = constant, R is universal gas constant)
The work done in a minuscule isothermal expansion is given by
dW = PdV ...(ii)
The total work done in completing the expansion from initial volume vi to final volume Vf is denoted by
`W = int_(v_i)^(v_f) PdV`
∴ `W = nRT int_(v_i)^(v_f) (dV)/V` ...[from(i)]
∴ W = nRT [In Vf - InVi]
∴ W = nRT In `V_f/V_i`
∴ W = 2.303 nRT `log_10 V_f/V_i`
उत्तर २
Consider the isothermal expansion of an ideal gas. During this process, small work is done, and it is given by
dW = PdV
We get the total work done by integrating the above equation with the limit Vi to Vf.
`W = int_(V_i)^(V_f)Pdv` ...(i)
But we know that for an ideal gas, PV = nRT.
∴ Equation (i) becomes,
`W = int_(V_i)^(V_f)(nRT)/V dV`
`W = nRT int_(V_i)^(V_f)(dV)/V`
`W = nRT [log V]_(V_i)^(V_f)`
`W = nRT log_e (V_f/V_i)`
or `W = 2.303 nRT log_10 (V_f/V_i)`
APPEARS IN
संबंधित प्रश्न
Write the mathematical expression of the First Law of Thermodynamics for the Isobaric process.
When we heat an object, it expands. Is work done by the object in this process? Is heat given to the object equal to the increase in its internal energy?
Refer to figure. Let ∆U1 and ∆U2 be the change in internal energy in processes A and B respectively, ∆Q be the net heat given to the system in process A + B and ∆W be the net work done by the system in the process A + B.

(a) ∆U1 + ∆U2 = 0
(b) ∆U1 − ∆U2 = 0
(c) ∆Q − ∆W = 0
(d) ∆Q + ∆W = 0
A thermally insulated, closed copper vessel contains water at 15°C. When the vessel is shaken vigorously for 15 minutes, the temperature rises to 17°C. The mass of the vessel is 100 g and that of the water is 200 g. The specific heat capacities of copper and water are 420 J kg−1 K−1 and 4200 J kg−1 K−1 respectively. Neglect any thermal expansion. (a) How much heat is transferred to the liquid-vessel system? (b) How much work has been done on this system? (c) How much is the increase in internal energy of the system?
The pressure of a gas changes linearly with volume from 10 kPa, 200 cc to 50 kPa, 50 cc. (a) Calculate the work done by the gas. (b) If no heat is supplied or extracted from the gas, what is the change in the internal energy of the gas?
A gas is enclosed in a cylindrical vessel fitted with a frictionless piston. The gas is slowly heated for some time. During the process, 10 J of heat is supplied and the piston is found to move out 10 cm. Find the increase in the internal energy of the gas. The area of cross section of the cylinder = 4 cm2 and the atmospheric pressure = 100 kPa.
Calculate the increase in the internal energy of 10 g of water when it is heated from 0°C to 100°C and converted into steam at 100 kPa. The density of steam = 0.6 kg m−3. Specific heat capacity of water = 4200 J kg−1 °C−1 and the latent heat of vaporization of water = 2.25 × 10 6J kg−1.
A resistor held in running water carries electric current. Treat the resistor as the system
- Does heat flow into the resistor?
- Is there a flow of heat into the water?
- Is any work done?
- Assuming the state of resistance to remain unchanged, apply the first law of thermodynamics to this process.
For an Isothermal process
Define an isolated system.
Which of the following are TRUE for a reversible isothermal process?
(i) ∆U = 0
(ii) ∆H = 0
(iii) Q = W
(iv) ∆T = 0
A gas performs 0.320 kJ work on surrounding and absorbs 120 J of heat from the surrounding. Hence, change in internal energy is ______.
Based on first law of thermodynamics which of the following is correct.
120 J of heat is added to a gaseous system, whose internal energy change is 60 J, then the amount of external work done is ____________.
Calculate the amount of work done during isothermal expansion of a gas from a volume of 4 dm3 to 6 dm3 against a constant external pressure of 3 atmosphere?
Change in internal energy, when 4 KJ of work is done on the system and 1 KJ heat is given out by the system, is:
An ideal gas undergoes cyclic process ABCDA as shown in given P-V diagram (figure). The amount of work done by the gas is ______.

Consider two containers A and B containing identical gases at the same pressure, volume and temperature. The gas in container A is compressed to half of its original volume isothermally while the gas in container B is compressed to half of its original value adiabatically. The ratio of final pressure of gas in B to that of gas in A is ______.
Can a system be heated and its temperature remains constant?
Consider that an ideal gas (n moles) is expanding in a process given by P = f(V), which passes through a point (V0, P0). Show that the gas is absorbing heat at (P0, V0) if the slope of the curve P = f(V) is larger than the slope of the adiabat passing through (P0, V0).
Consider one mole of perfect gas in a cylinder of unit cross section with a piston attached (figure). A spring (spring constant k) is attached (unstretched length L) to the piston and to the bottom of the cylinder. Initially the spring is unstretched and the gas is in equilibrium. A certain amount of heat Q is supplied to the gas causing an increase of volume from V0 to V1.
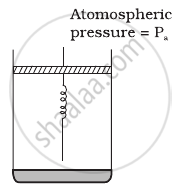
- What is the initial pressure of the system?
- What is the final pressure of the system?
- Using the first law of thermodynamics, write down a relation between Q, Pa, V, Vo and k.
ΔU = 0 is true for ______.
What work will be done, when 3 moles of an ideal gas are compressed to half the initial volume at a constant temperature of 300 K?
An ideal gas having pressure p, volume V and temperature T undergoes a thermodynamic process in which dW = 0 and dQ < 0. Then, for the gas ______.
A given system undergoes a change in which the work done by the system equals the decrease in its internal energy. The system must have undergone an ______.
In an adiabatic process, W = ______.
In an adiabatic expansion of 2 moles of a gas, the initial pressure was 1.013 × 105 Pa, the initial volume was 22.4 L, the final pressure was 3.191 × 104 Pa and the final volume was 44.8 L. Find the work done by the gas on its surroundings. Taken `γ = 5/3`.
Define isochoric process
