Advertisements
Advertisements
प्रश्न
Obtain an expression for the workdone by a gas in an isothermal process.
उत्तर १
Work done by a gas in an isothermal process:
Consider the moles of a gas contained within a cylinder with a moveable, light, and frictionless piston. Let Pi, Vi, and T represent the gas's initial pressure, volume, and absolute temperature, respectively.
Consider an isothermal expansion (or compression) of a gas, where Pf, vf, and T are the final pressure, volume, and absolute temperature of the gas, respectively.
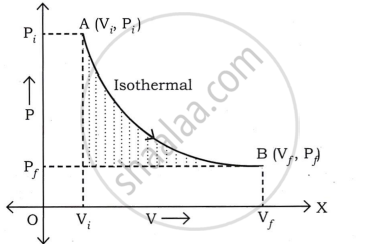
For an isothermal change,
PiVi = PfVf = constant
If the gas behaves like an ideal gas, its equation of state is
PV = nRT = constant ...(i) ....(as T = constant, R is universal gas constant)
The work done in a minuscule isothermal expansion is given by
dW = PdV ...(ii)
The total work done in completing the expansion from initial volume vi to final volume Vf is denoted by
`W = int_(v_i)^(v_f) PdV`
∴ `W = nRT int_(v_i)^(v_f) (dV)/V` ...[from(i)]
∴ W = nRT [In Vf - InVi]
∴ W = nRT In `V_f/V_i`
∴ W = 2.303 nRT `log_10 V_f/V_i`
उत्तर २
Consider the isothermal expansion of an ideal gas. During this process, small work is done, and it is given by
dW = PdV
We get the total work done by integrating the above equation with the limit Vi to Vf.
`W = int_(V_i)^(V_f)Pdv` ...(i)
But we know that for an ideal gas, PV = nRT.
∴ Equation (i) becomes,
`W = int_(V_i)^(V_f)(nRT)/V dV`
`W = nRT int_(V_i)^(V_f)(dV)/V`
`W = nRT [log V]_(V_i)^(V_f)`
`W = nRT log_e (V_f/V_i)`
or `W = 2.303 nRT log_10 (V_f/V_i)`
APPEARS IN
संबंधित प्रश्न
Write the mathematical expression of the First Law of Thermodynamics for the Isobaric process.
Refer to figure. Let ∆U1 and ∆U2 be the change in internal energy in processes A and B respectively, ∆Q be the net heat given to the system in process A + B and ∆W be the net work done by the system in the process A + B.

(a) ∆U1 + ∆U2 = 0
(b) ∆U1 − ∆U2 = 0
(c) ∆Q − ∆W = 0
(d) ∆Q + ∆W = 0
The pressure of a gas changes linearly with volume from 10 kPa, 200 cc to 50 kPa, 50 cc. (a) Calculate the work done by the gas. (b) If no heat is supplied or extracted from the gas, what is the change in the internal energy of the gas?
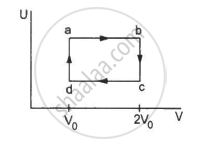
Figure shows the variation in the internal energy U with the volume V of 2.0 mol of an ideal gas in a cyclic process abcda. The temperatures of the gas at b and c are 500 K and 300 K respectively. Calculate the heat absorbed by the gas during the process.
Calculate the increase in the internal energy of 10 g of water when it is heated from 0°C to 100°C and converted into steam at 100 kPa. The density of steam = 0.6 kg m−3. Specific heat capacity of water = 4200 J kg−1 °C−1 and the latent heat of vaporization of water = 2.25 × 10 6J kg−1.
An adiabatic vessel of total volume V is divided into two equal parts by a conducting separator. The separator is fixed in this position. The part on the left contains one mole of an ideal gas (U = 1.5 nRT) and the part on the right contains two moles of the same gas. Initially, the pressure on each side is p. The system is left for sufficient time so that a steady state is reached. Find (a) the work done by the gas in the left part during the process, (b) the temperature on the two sides in the beginning, (c) the final common temperature reached by the gases, (d) the heat given to the gas in the right part and (e) the increase in the internal energy of the gas in the left part.
Define an isolated system.
Two moles of an ideal gas is expanded isothermally and reversibly at 300 K from 1 L to 10 L. The enthalpy change in kJ is ______.
The process, in which no heat enters or leaves the system, is termed as ____________.
In a given process for an ideal gas, dW = 0 and dQ < 0. Then for the gas ____________.
The isothermal bulk modulus of a perfect gas at pressure P is numerically equal to ____________.
Change in internal energy, when 4 KJ of work is done on the system and 1 KJ heat is given out by the system, is:
Air pressure in a car tyre increases during driving. Explain.
In the reported figure, heat energy absorbed by a system in going through a cyclic process is ______ πJ.
An electric appliance supplies 6000 J/min heat to the system. If the system delivers a power of 90 W. How long it would take to increase the internal energy by 2.5 × 103 J?
200g water is heated from 40°C to 60°C. Ignoring the slight expansion of water, the change in its internal energy is close to ______.
(Given specific heat of water = 4184 J/kgK)
Mathematical equation of first law of thermodynamics for isochoric process is ______.
An ideal gas (γ = 1.5) is expanded adiabatically. How many times has the gas had to be expanded to reduce the root mean square velocity of molecules two times?
One mole of an ideal gas is initially kept in a cylinder with a movable frictionless and massless piston at pressure of 1.01MPa, and temperature 27°C. It is then expanded till its volume is doubled. How much work is done if the expansion is isobaric?
In an adiabatic process, ______.
In an adiabatic process, W = ______.
For an isothermal and reversible expansion of 0.5 mol of an ideal gas Wmax is - 3.918 kJ. The value of ΔU is ______.
In an adiabatic expansion of 2 moles of a gas, the initial pressure was 1.013 × 105 Pa, the initial volume was 22.4 L, the final pressure was 3.191 × 104 Pa and the final volume was 44.8 L. Find the work done by the gas on its surroundings. Taken `γ = 5/3`.
What is Isobaric process?
Define isochoric process
