Advertisements
Advertisements
प्रश्न
An adiabatic vessel of total volume V is divided into two equal parts by a conducting separator. The separator is fixed in this position. The part on the left contains one mole of an ideal gas (U = 1.5 nRT) and the part on the right contains two moles of the same gas. Initially, the pressure on each side is p. The system is left for sufficient time so that a steady state is reached. Find (a) the work done by the gas in the left part during the process, (b) the temperature on the two sides in the beginning, (c) the final common temperature reached by the gases, (d) the heat given to the gas in the right part and (e) the increase in the internal energy of the gas in the left part.
उत्तर
(a) Since the conducting wall is fixed, the work done by the gas on the left part during the process is zero because the change in volume will be zero due to the fixed position of the wall.
(b) For left side:-
Let the initial pressure on both sides of the wall be p.
We know,
Volume = \[\frac{V}{2}\]
Number of moles, n = 1
Let initial temperature be T1.
Using the ideal gas equation, we get
\[\frac{PV}{2} = nR T_1 \]
\[ \Rightarrow \frac{PV}{2} = (1) RT\]
\[ \Rightarrow T_1 = \frac{PV}{(2 \text{moles}) R}\]
For right side:-
Number of moles, n = 2
Let the initial temperature be T2.
We know,
Volume = \[\frac{V}{2}\]
\[\frac{PV}{2} = nR T_2 \]
\[ \Rightarrow T_2 = \frac{PV}{(4 \text{moles}) R}\]
(c)
Here,
U = 1.5nRT
T = temperature at the equilibrium
P1 = P2 = P
n1 = 1 mol
n2 = 2 mol
Let T1 and T2 be the initial temperatures of the left and right chamber respectively.
Applying eqn. of state
For left side chamber
`PV/2=n_1RT_1`
`rArrPV/2=RT_1`
`rArr PV = 2RT_1`
`rArrT_1=(PV)/(2R)`
Right side chamber
`PV/2=n_2RT_2`
`rArrPV/2=2RT_2`
`rArrT_2=(PV)/(4R)`
We know that total n = n1 + n2 = 3
U1 = n1CvT1 = CvT1
U2 = n2CvT2 = 2CvT2
U =nCvT
U = U1 + U2
`rArr3C_"v"T=C_"v"T_1+2C_"v"T_2`
`rArr3T=T_1+2T_2`
`rArr3T=(PV)/(2R)+(2PV)/(4R)`
`rArrT=(PV)/(3R)`
(d) For RHS:-
∆Q = ∆U as ∆W = 0
∆U = 1.5 n2R (T − T2)
When T is the final temperature and T2 is the initial temperature of side 1, we get
= 1.5 × 2 × R (T − T2)
= 1.5 × 2 × \[\frac{4PV - 3PV}{4 \times 3 \text{mole}}\]
\[= \frac{3 \times PV}{4 \times 3 \text{mole}} = \frac{PV}{4}\]
(e) If dW = 0, then using the first law, we get
dQ = − dU
⇒ dU = − dQ = \[\frac{- PV}{4}\]
APPEARS IN
संबंधित प्रश्न
When we heat an object, it expands. Is work done by the object in this process? Is heat given to the object equal to the increase in its internal energy?
The pressure of a gas changes linearly with volume from 10 kPa, 200 cc to 50 kPa, 50 cc. (a) Calculate the work done by the gas. (b) If no heat is supplied or extracted from the gas, what is the change in the internal energy of the gas?
Calculate the heat absorbed by a system in going through the cyclic process shown in figure.
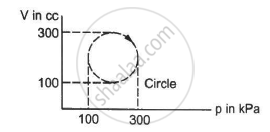
ΔU is equal to ____________ work.
When heat energy of 2000 joules is supplied to a gas at constant pressure 2.1 x 105 N/m2, there is an increase in its volume equal to 2.5 x 10-3 m3. The increase in internal energy of the gas in joules is ____________.
"The mass and energy both are conserved in an isolated system", is the statement of ______.
A gas performs 0.320 kJ work on surrounding and absorbs 120 J of heat from the surrounding. Hence, change in internal energy is ______.
A sample of gas absorbs 4000 kJ of heat and surrounding does 2000 J of work on sample, what is the value of ΔU?
Consider two containers A and B containing identical gases at the same pressure, volume and temperature. The gas in container A is compressed to half of its original volume isothermally while the gas in container B is compressed to half of its original value adiabatically. The ratio of final pressure of gas in B to that of gas in A is ______.
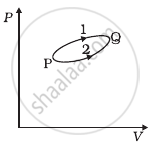
A system goes from P to Q by two different paths in the P-V diagram as shown in figure. Heat given to the system in path 1 is 1000 J. The work done by the system along path 1 is more than path 2 by 100 J. What is the heat exchanged by the system in path 2?
Write the mathematical equation for the first law of thermodynamics for:
Adiabatic process
The amount of heat needed to raise the temperature of 4 moles of a rigid diatomic gas from 0°C to 50°C when no work is done is ______.
(R is the universal gas constant.)
An insulated container of gas has two chambers separated by an insulating partition. One of the chambers has volume V1 and contains ideal gas at pressure P1 and temperature T1. The other chamber has volume V2 and contains ideal gas at pressure P2 and temperature T2. If the partition is removed without doing any work on the gas, the final equilibrium temperature of the gas in the container will be ______.
A soap bubble in vacuum has a radius of 3 cm and another soap bubble in vacuum has a radius of 4 cm. If the two bubbles coalesce under isothermal condition, then the radius of the new bubble is ______.
In an adiabatic process, ______.
Explain the formulation of first law of thrmodynamics.
Choose the correct relation with reason.
Write a short note on isobar.
Define the isothermal process.
