Advertisements
Advertisements
Question
An adiabatic vessel of total volume V is divided into two equal parts by a conducting separator. The separator is fixed in this position. The part on the left contains one mole of an ideal gas (U = 1.5 nRT) and the part on the right contains two moles of the same gas. Initially, the pressure on each side is p. The system is left for sufficient time so that a steady state is reached. Find (a) the work done by the gas in the left part during the process, (b) the temperature on the two sides in the beginning, (c) the final common temperature reached by the gases, (d) the heat given to the gas in the right part and (e) the increase in the internal energy of the gas in the left part.
Solution
(a) Since the conducting wall is fixed, the work done by the gas on the left part during the process is zero because the change in volume will be zero due to the fixed position of the wall.
(b) For left side:-
Let the initial pressure on both sides of the wall be p.
We know,
Volume = \[\frac{V}{2}\]
Number of moles, n = 1
Let initial temperature be T1.
Using the ideal gas equation, we get
\[\frac{PV}{2} = nR T_1 \]
\[ \Rightarrow \frac{PV}{2} = (1) RT\]
\[ \Rightarrow T_1 = \frac{PV}{(2 \text{moles}) R}\]
For right side:-
Number of moles, n = 2
Let the initial temperature be T2.
We know,
Volume = \[\frac{V}{2}\]
\[\frac{PV}{2} = nR T_2 \]
\[ \Rightarrow T_2 = \frac{PV}{(4 \text{moles}) R}\]
(c)
Here,
U = 1.5nRT
T = temperature at the equilibrium
P1 = P2 = P
n1 = 1 mol
n2 = 2 mol
Let T1 and T2 be the initial temperatures of the left and right chamber respectively.
Applying eqn. of state
For left side chamber
`PV/2=n_1RT_1`
`rArrPV/2=RT_1`
`rArr PV = 2RT_1`
`rArrT_1=(PV)/(2R)`
Right side chamber
`PV/2=n_2RT_2`
`rArrPV/2=2RT_2`
`rArrT_2=(PV)/(4R)`
We know that total n = n1 + n2 = 3
U1 = n1CvT1 = CvT1
U2 = n2CvT2 = 2CvT2
U =nCvT
U = U1 + U2
`rArr3C_"v"T=C_"v"T_1+2C_"v"T_2`
`rArr3T=T_1+2T_2`
`rArr3T=(PV)/(2R)+(2PV)/(4R)`
`rArrT=(PV)/(3R)`
(d) For RHS:-
∆Q = ∆U as ∆W = 0
∆U = 1.5 n2R (T − T2)
When T is the final temperature and T2 is the initial temperature of side 1, we get
= 1.5 × 2 × R (T − T2)
= 1.5 × 2 × \[\frac{4PV - 3PV}{4 \times 3 \text{mole}}\]
\[= \frac{3 \times PV}{4 \times 3 \text{mole}} = \frac{PV}{4}\]
(e) If dW = 0, then using the first law, we get
dQ = − dU
⇒ dU = − dQ = \[\frac{- PV}{4}\]
APPEARS IN
RELATED QUESTIONS
The internal energy of an ideal gas decreases by the same amount as the work done by the system.
(a) The process must be adiabatic.
b) The process must be isothermal.
(c) The process must be isobaric.
(d) The temperature must decrease.
A gas is enclosed in a cylindrical vessel fitted with a frictionless piston. The gas is slowly heated for some time. During the process, 10 J of heat is supplied and the piston is found to move out 10 cm. Find the increase in the internal energy of the gas. The area of cross section of the cylinder = 4 cm2 and the atmospheric pressure = 100 kPa.
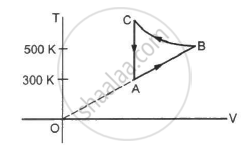
Consider the cyclic process ABCA, shown in figure, performed on a sample of 2.0 mol of an ideal gas. A total of 1200 J of heat is withdrawn from the sample in the process. Find the work done by the gas during the part BC.
ΔU is equal to ____________ work.
A sample of gas absorbs 4000 kJ of heat and surrounding does 2000 J of work on sample. What is the value of ∆U?
Two moles of an ideal gas is expanded isothermally and reversibly at 300 K from 1 L to 10 L. The enthalpy change in kJ is ______.
"The mass and energy both are conserved in an isolated system", is the statement of ______.
Change in internal energy, when 4 KJ of work is done on the system and 1 KJ heat is given out by the system, is:
Three copper blocks of masses M1, M2 and M3 kg respectively are brought into thermal contact till they reach equilibrium. Before contact, they were at T1, T2, T3 (T1 > T2 > T3). Assuming there is no heat loss to the surroundings, the equilibrium temprature T is (s is specific heat of copper)
A cycle followed by an engine (made of one mole of perfect gas in a cylinder with a piston) is shown in figure.
A to B : volume constant
B to C : adiabatic
C to D : volume constant
D to A : adiabatic
VC = VD = 2VA = 2VB
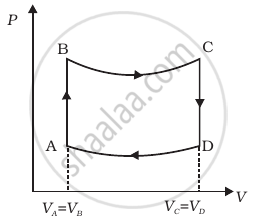
- In which part of the cycle heat is supplied to the engine from outside?
- In which part of the cycle heat is being given to the surrounding by the engine?
- What is the work done by the engine in one cycle? Write your answer in term of PA, PB, VA.
- What is the efficiency of the engine?
(γ = `5/3` for the gas), (Cv = `3/2` R for one mole)
A cycle followed by an engine (made of one mole of an ideal gas in a cylinder with a piston) is shown in figure. Find heat exchanged by the engine, with the surroundings for each section of the cycle. (Cv = (3/2)R)
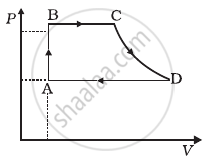
- AB : constant volume
- BC : constant pressure
- CD : adiabatic
- DA : constant pressure
Mathematical equation of first law of thermodynamics for isochoric process is ______.
The first law of thermodynamics for isothermal process is ______.
If one mole of monoatomic gas `(gamma=5/3)` is mixed with one mole of diatomic gas `(gamma=7/5)`, the value of γ for the mixture is ______.
ΔU = 0 is true for ______.
A given system undergoes a change in which the work done by the system equals the decrease in its internal energy. The system must have undergone an ______.
In an adiabatic expansion of 2 moles of a gas, the initial pressure was 1.013 × 105 Pa, the initial volume was 22.4 L, the final pressure was 3.191 × 104 Pa and the final volume was 44.8 L. Find the work done by the gas on its surroundings. Taken `γ = 5/3`.
A monoatomic gas at 27°C is adiabatically compressed to 80% of its initial volume. Find the final temperature of the gas.
Choose the correct relation with reason.
