Advertisements
Advertisements
Question
Consider the cyclic process ABCA, shown in figure, performed on a sample of 2.0 mol of an ideal gas. A total of 1200 J of heat is withdrawn from the sample in the process. Find the work done by the gas during the part BC.
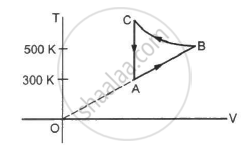
Solution
Given:-
Number of moles of the gas, n = 2
∆Q = − 1200 J (Negative sign shows that heat is extracted out from the system)
∆U = 0 ..............(During cyclic process)
Using the first law of thermodynamics, we get
∆Q = ∆U + ∆W
⇒ −1200 = 0 + (WAB + WBC + WCA)
Since the change in volume of the system applies on line CA, work done during CA will be zero.
From the ideal gas equation, we get
PV = nRT
P∆V = nR∆T
W = P∆V = nR∆T
⇒ ∆Q = ∆U + ∆W
⇒ −1200 = nR∆T + WBC + 0
⇒ −1200 = 2 × 8.3 × 200 + WBC
WBC = − 400 × 8.3 − 1200
= − 4520 J
APPEARS IN
RELATED QUESTIONS
50 cal of heat should be supplied to take a system from the state A to the state B through the path ACB as shown in figure. Find the quantity of heat to be suppled to take it from A to B via ADB.

A gas is enclosed in a cylindrical vessel fitted with a frictionless piston. The gas is slowly heated for some time. During the process, 10 J of heat is supplied and the piston is found to move out 10 cm. Find the increase in the internal energy of the gas. The area of cross section of the cylinder = 4 cm2 and the atmospheric pressure = 100 kPa.
A resistor held in running water carries electric current. Treat the resistor as the system
- Does heat flow into the resistor?
- Is there a flow of heat into the water?
- Is any work done?
- Assuming the state of resistance to remain unchanged, apply the first law of thermodynamics to this process.
For an Isochoric process
For a particular reaction, the system absorbs 8 kJ of heat and does 2.5 kJ of work on its surrounding. What will be the change in internal energy of the system?
Change in internal energy, when 4 KJ of work is done on the system and 1 KJ heat is given out by the system, is:
Is it possible to increase the temperature of a gas without adding heat to it? Explain.
Consider a cycle tyre being filled with air by a pump. Let V be the volume of the tyre (fixed) and at each stroke of the pump ∆V(V) of air is transferred to the tube adiabatically. What is the work done when the pressure in the tube is increased from P1 to P2?
Consider a P-V diagram in which the path followed by one mole of perfect gas in a cylindrical container is shown in figure.
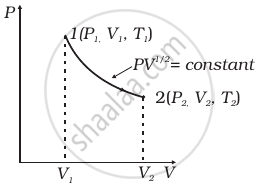
- Find the work done when the gas is taken from state 1 to state 2.
- What is the ratio of temperature T1/T2, if V2 = 2V1?
- Given the internal energy for one mole of gas at temperature T is (3/2) RT, find the heat supplied to the gas when it is taken from state 1 to 2, with V2 = 2V1.
Consider that an ideal gas (n moles) is expanding in a process given by P = f(V), which passes through a point (V0, P0). Show that the gas is absorbing heat at (P0, V0) if the slope of the curve P = f(V) is larger than the slope of the adiabat passing through (P0, V0).
Consider one mole of perfect gas in a cylinder of unit cross section with a piston attached (figure). A spring (spring constant k) is attached (unstretched length L) to the piston and to the bottom of the cylinder. Initially the spring is unstretched and the gas is in equilibrium. A certain amount of heat Q is supplied to the gas causing an increase of volume from V0 to V1.
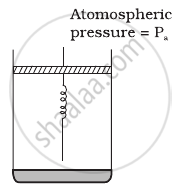
- What is the initial pressure of the system?
- What is the final pressure of the system?
- Using the first law of thermodynamics, write down a relation between Q, Pa, V, Vo and k.
200g water is heated from 40°C to 60°C. Ignoring the slight expansion of water, the change in its internal energy is close to ______.
(Given specific heat of water = 4184 J/kgK)
An insulated container of gas has two chambers separated by an insulating partition. One of the chambers has volume V1 and contains ideal gas at pressure P1 and temperature T1. The other chamber has volume V2 and contains ideal gas at pressure P2 and temperature T2. If the partition is removed without doing any work on the gas, the final equilibrium temperature of the gas in the container will be ______.
One mole of an ideal gas is allowed to expand reversibly and adiabatically from a temperature of 27°C. If the work done during the process is 3 kJ, the final temperature will be equal to ______.
(Cv = 20 JK−1)
The V cc volume of gas having `γ = 5/2` is suddenly compressed to `(V/4)` cc. The initial pressure of the gas is p. The final pressure of the gas will be ______.
An ideal gas (γ = 1.5) is expanded adiabatically. How many times has the gas had to be expanded to reduce the root mean square velocity of molecules two times?
One mole of an ideal gas is initially kept in a cylinder with a movable frictionless and massless piston at pressure of 1.01MPa, and temperature 27°C. It is then expanded till its volume is doubled. How much work is done if the expansion is isobaric?
If the adiabatic ratio for a gas is 5/3, find the molar specific heat capacity of the gas at (i) constant volume (ii) constant pressure.
Using the first law of thermodynamics, show that for an ideal gas, the difference between the molar specific heat capacities at constant pressure and at constant volume is equal to the molar gas constant R.
What is an isothermal process?
