Advertisements
Advertisements
Question
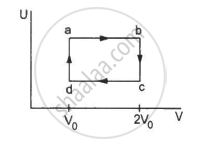
Figure shows the variation in the internal energy U with the volume V of 2.0 mol of an ideal gas in a cyclic process abcda. The temperatures of the gas at b and c are 500 K and 300 K respectively. Calculate the heat absorbed by the gas during the process.
Solution
Given: Number of moles of the gas, n = 2 moles
The system's volume is constant for lines bc and da.
Therefore,
∆V = 0
Thus, work done for paths da and bc is zero.
⇒ Wda = Wbc = 0
Since the process is cyclic, ∆U is equal to zero.
Using the first law, we get
∆W = ∆Q
∆W = ∆WAB + ∆WCD
Since the temperature is kept constant during lines ab and cd, these are isothermal expansions.
Work done during an isothermal process is given by
W = nRT
\[\ln\frac{V_f}{V_i}\]
If Vf and Vi are the initial and final volumes during the isothermal process, then
\[W = n {RT}_1 ln\left( \frac{2 V_0}{V_0} \right) + n {RT}_2 ln\left( \frac{V_0}{2 V_0} \right)\]
W = nR × 2.303 × log 2 × (500 − 300)
W = 2 × 8.314 × 2.303 × 0.301 × 200
W = 2305.31 J
APPEARS IN
RELATED QUESTIONS
Write the mathematical expression of the First Law of Thermodynamics for the Isobaric process.
When we heat an object, it expands. Is work done by the object in this process? Is heat given to the object equal to the increase in its internal energy?
The pressure of a gas changes linearly with volume from 10 kPa, 200 cc to 50 kPa, 50 cc. (a) Calculate the work done by the gas. (b) If no heat is supplied or extracted from the gas, what is the change in the internal energy of the gas?
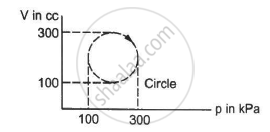
Calculate the heat absorbed by a system in going through the cyclic process shown in figure.
The internal energy of a gas is given by U = 1.5 pV. It expands from 100 cm3 to 200 cm3against a constant pressure of 1.0 × 105 Pa. Calculate the heat absorbed by the gas in the process.
A gas is enclosed in a cylindrical vessel fitted with a frictionless piston. The gas is slowly heated for some time. During the process, 10 J of heat is supplied and the piston is found to move out 10 cm. Find the increase in the internal energy of the gas. The area of cross section of the cylinder = 4 cm2 and the atmospheric pressure = 100 kPa.
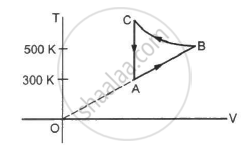
Consider the cyclic process ABCA, shown in figure, performed on a sample of 2.0 mol of an ideal gas. A total of 1200 J of heat is withdrawn from the sample in the process. Find the work done by the gas during the part BC.
Find the change in the internal energy of 2 kg of water as it is heated from 0°C to 4°C. The specific heat capacity of water is 4200 J kg−1 K−1 and its densities at 0°C and 4°C are 999.9 kg m−3 and 1000 kg m−3 respectively. Atmospheric pressure = 105 Pa.
A gas performs 0.320 kJ work on surrounding and absorbs 120 J of heat from the surrounding. Hence, change in internal energy is ______.
120 J of heat is added to a gaseous system, whose internal energy change is 60 J, then the amount of external work done is ____________.
For a particular reaction, the system absorbs 8 kJ of heat and does 2.5 kJ of work on its surrounding. What will be the change in internal energy of the system?
The isothermal bulk modulus of a perfect gas at pressure P is numerically equal to ____________.
Can a system be heated and its temperature remains constant?
The initial state of a certain gas is (Pi, Vi, Ti). It undergoes expansion till its volume becomes Vf. Consider the following two cases:
- the expansion takes place at constant temperature.
- the expansion takes place at constant pressure.
Plot the P-V diagram for each case. In which of the two cases, is the work done by the gas more?
The first law of thermodynamics for isothermal process is ______.
A given system undergoes a change in which the work done by the system equals the decrease in its internal energy. The system must have undergone an ______.
What is Isobaric process?
Consider the cyclic process ABCA on a sample of 2.0 mol of an ideal gas as shown in following figure. The temperature of the gas at A and B are 300 K and 500 K respectively. A total of 1200 J heat is withdrawn from the sample in this process. Find the work done by the gas in part BC. (R = 8.3 J/mol K)
A monoatomic gas at 27°C is adiabatically compressed to 80% of its initial volume. Find the final temperature of the gas.
Write a short note on isobar.
