Advertisements
Advertisements
Question
When we heat an object, it expands. Is work done by the object in this process? Is heat given to the object equal to the increase in its internal energy?
Solution
When we heat an object, it expands, i.e. its volume increases.
Work done by the system, ΔW = P Δ V
Using the first law of thermodynamics, we get
ΔQ = ΔU + ΔW
Since the volume changes, ΔW has some non-zero positive value. Thus, heat given to the object is not equal to the increase in the internal energy of the system.
APPEARS IN
RELATED QUESTIONS
An electric heater supplies heat to a system at a rate of 100W. If the system performs work at a rate of 75 Joules per second. At what rate is the internal energy increasing?
50 cal of heat should be supplied to take a system from the state A to the state B through the path ACB as shown in figure. Find the quantity of heat to be suppled to take it from A to B via ADB.

A resistor held in running water carries electric current. Treat the resistor as the system
- Does heat flow into the resistor?
- Is there a flow of heat into the water?
- Is any work done?
- Assuming the state of resistance to remain unchanged, apply the first law of thermodynamics to this process.
A sample of gas absorbs 4000 kJ of heat and surrounding does 2000 J of work on sample. What is the value of ∆U?
For a particular reaction, the system absorbs 8 kJ of heat and does 2.5 kJ of work on its surrounding. What will be the change in internal energy of the system?
A sample of gas absorbs 4000 kJ of heat and surrounding does 2000 J of work on sample, what is the value of ΔU?
Consider two containers A and B containing identical gases at the same pressure, volume and temperature. The gas in container A is compressed to half of its original volume isothermally while the gas in container B is compressed to half of its original value adiabatically. The ratio of final pressure of gas in B to that of gas in A is ______.
An ideal gas undergoes isothermal process from some initial state i to final state f. Choose the correct alternatives.
- dU = 0
- dQ= 0
- dQ = dU
- dQ = dW
A system goes from P to Q by two different paths in the P-V diagram as shown in figure. Heat given to the system in path 1 is 1000 J. The work done by the system along path 1 is more than path 2 by 100 J. What is the heat exchanged by the system in path 2?
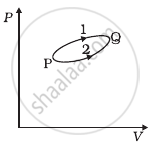
A cycle followed by an engine (made of one mole of an ideal gas in a cylinder with a piston) is shown in figure. Find heat exchanged by the engine, with the surroundings for each section of the cycle. (Cv = (3/2)R)
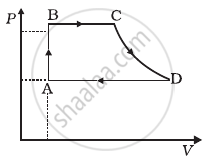
- AB : constant volume
- BC : constant pressure
- CD : adiabatic
- DA : constant pressure
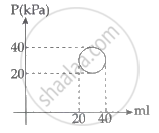
In the reported figure, heat energy absorbed by a system in going through a cyclic process is ______ πJ.
An insulated container of gas has two chambers separated by an insulating partition. One of the chambers has volume V1 and contains ideal gas at pressure P1 and temperature T1. The other chamber has volume V2 and contains ideal gas at pressure P2 and temperature T2. If the partition is removed without doing any work on the gas, the final equilibrium temperature of the gas in the container will be ______.
One mole of an ideal gas is allowed to expand reversibly and adiabatically from a temperature of 27°C. If the work done during the process is 3 kJ, the final temperature will be equal to ______.
(Cv = 20 JK−1)
The amount of work done in increasing the voltage across the plates of capacitor from 5 V to 10 V is W. The work done in increasing it from 10 V to 15 V will be ______.
104 J of work is done on a certain volume of a gas. If the gas releases 125 kJ of heat, calculate the change in internal energy of the gas.
Consider the cyclic process ABCA on a sample of 2.0 mol of an ideal gas as shown in following figure. The temperature of the gas at A and B are 300 K and 500 K respectively. A total of 1200 J heat is withdrawn from the sample in this process. Find the work done by the gas in part BC. (R = 8.3 J/mol K)
A monoatomic gas at 27°C is adiabatically compressed to 80% of its initial volume. Find the final temperature of the gas.
