Advertisements
Advertisements
Question
50 cal of heat should be supplied to take a system from the state A to the state B through the path ACB as shown in figure. Find the quantity of heat to be suppled to take it from A to B via ADB.

Solution
Given:-
In path ACB,
∆Q = 50 cal = (50 × 4.2) J
∆Q = 210 J
∆W = WAC + WCB
Since initial and final volumes are the same along the line BC, change in volume of the system along BC is zero.
Hence, work done along this line will be zero.
For line AC:-
P = 50 kPa
Volume changes from 200 cc to 400 cc.
`rArrDelta V =400-200c c=200 c c`
∆W = WAC + WCB
= 50 × 10−3 × 200 × 10−6 + 0
= 10 J
Using the first law of thermodynamics, we get
∆Q = ∆U + ∆W
⇒ ∆U = ∆Q − ∆W = (210 − 10) J
∆U = 200 J
In path ADB, ∆Q = ?
∆U = 200 J ..............(Internal energy depends only on the initial and final points and not on the path followed.)
⇒ ∆W = WAD + WDB = ∆W
Work done for line AD will also be zero.
For line DB:-
P = 155 kPa
`rArrDelta V =400-200c c=200 c c`
W = 0 + 155 × 103 × 200 × 10−6
W = 31 J
∆Q = ∆U + ∆W
∆Q= (200 + 31) J = 231 J
∆Q = 55 cal
APPEARS IN
RELATED QUESTIONS
Write the mathematical expression of the First Law of Thermodynamics for the Isobaric process.
The internal energy of an ideal gas decreases by the same amount as the work done by the system.
(a) The process must be adiabatic.
b) The process must be isothermal.
(c) The process must be isobaric.
(d) The temperature must decrease.
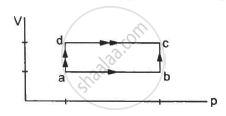
When a system is taken through the process abc shown in figure, 80 J of heat is absorbed by the system and 30 J of work is done by it. If the system does 10 J of work during the process adc, how much heat flows into it during the process?
A gas is enclosed in a cylindrical vessel fitted with a frictionless piston. The gas is slowly heated for some time. During the process, 10 J of heat is supplied and the piston is found to move out 10 cm. Find the increase in the internal energy of the gas. The area of cross section of the cylinder = 4 cm2 and the atmospheric pressure = 100 kPa.
An adiabatic vessel of total volume V is divided into two equal parts by a conducting separator. The separator is fixed in this position. The part on the left contains one mole of an ideal gas (U = 1.5 nRT) and the part on the right contains two moles of the same gas. Initially, the pressure on each side is p. The system is left for sufficient time so that a steady state is reached. Find (a) the work done by the gas in the left part during the process, (b) the temperature on the two sides in the beginning, (c) the final common temperature reached by the gases, (d) the heat given to the gas in the right part and (e) the increase in the internal energy of the gas in the left part.
Answer the following in one or two sentences.
State the first law of thermodynamics.
A mixture of hydrogen and oxygen is enclosed in a rigid insulating cylinder. It is ignited by a spark. The temperature and pressure both increase considerably. Assume that the energy supplied by the spark is negligible, what conclusions may be drawn by application of the first law of thermodynamics?
ΔU is equal to ____________ work.
A gas performs 0.320 kJ work on surrounding and absorbs 120 J of heat from the surrounding. Hence, change in internal energy is ______.
For a particular reaction, the system absorbs 8 kJ of heat and does 2.5 kJ of work on its surrounding. What will be the change in internal energy of the system?
The isothermal bulk modulus of a perfect gas at pressure P is numerically equal to ____________.
Can a system be heated and its temperature remains constant?
A cycle followed by an engine (made of one mole of perfect gas in a cylinder with a piston) is shown in figure.
A to B : volume constant
B to C : adiabatic
C to D : volume constant
D to A : adiabatic
VC = VD = 2VA = 2VB
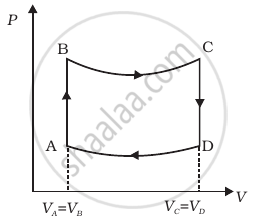
- In which part of the cycle heat is supplied to the engine from outside?
- In which part of the cycle heat is being given to the surrounding by the engine?
- What is the work done by the engine in one cycle? Write your answer in term of PA, PB, VA.
- What is the efficiency of the engine?
(γ = `5/3` for the gas), (Cv = `3/2` R for one mole)
Consider that an ideal gas (n moles) is expanding in a process given by P = f(V), which passes through a point (V0, P0). Show that the gas is absorbing heat at (P0, V0) if the slope of the curve P = f(V) is larger than the slope of the adiabat passing through (P0, V0).
Consider one mole of perfect gas in a cylinder of unit cross section with a piston attached (figure). A spring (spring constant k) is attached (unstretched length L) to the piston and to the bottom of the cylinder. Initially the spring is unstretched and the gas is in equilibrium. A certain amount of heat Q is supplied to the gas causing an increase of volume from V0 to V1.
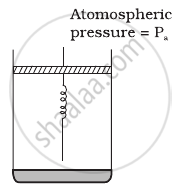
- What is the initial pressure of the system?
- What is the final pressure of the system?
- Using the first law of thermodynamics, write down a relation between Q, Pa, V, Vo and k.
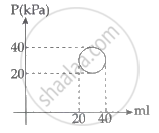
In the reported figure, heat energy absorbed by a system in going through a cyclic process is ______ πJ.
If one mole of monoatomic gas `(gamma=5/3)` is mixed with one mole of diatomic gas `(gamma=7/5)`, the value of γ for the mixture is ______.
A given system undergoes a change in which the work done by the system equals the decrease in its internal energy. The system must have undergone an ______.
104 J of work is done on a certain volume of a gas. If the gas releases 125 kJ of heat, calculate the change in internal energy of the gas.
Using the first law of thermodynamics, show that for an ideal gas, the difference between the molar specific heat capacities at constant pressure and at constant volume is equal to the molar gas constant R.
