Advertisements
Advertisements
Question
A resistor held in running water carries electric current. Treat the resistor as the system
- Does heat flow into the resistor?
- Is there a flow of heat into the water?
- Is any work done?
- Assuming the state of resistance to remain unchanged, apply the first law of thermodynamics to this process.
Solution
(a) The passage of electric current causes heat to be generated in the resistor. The heat generated = I2Rt in standard notation.
(b) Yes. The resistor generates heat in the water.
(c) \[\ce{\underset{(Q)}{I^2Rt} = \underset{(\Delta U)}{MCΔT} + \underset{(W)}{P \Delta V}}\]
Here, I = current through the resistor, R = resistance of the resistor, t = time for which the current is passed through the resistor, M = mass of the water, S = specific heat of water, T = rise in the temperature of water, P = pressure against which the work is done by the water, Δ V = increase in the volume of the water.
(d) There is no mention of the change in volume. So, there is no work done in this case.
∴ W = 0
First law of Thermodynamics,
ΔU = Q - W
The resistor is heated due to the joules heating effect. So, that it would transfer the heat to water. So, the amount of heat Q will be negative.
ΔU = - Q - 0
ΔU = - Q
RELATED QUESTIONS
Write the mathematical expression of the First Law of Thermodynamics for Isothermal Process
Write the mathematical expression of the First Law of Thermodynamics for the Isobaric process.
50 cal of heat should be supplied to take a system from the state A to the state B through the path ACB as shown in figure. Find the quantity of heat to be suppled to take it from A to B via ADB.

A gas is enclosed in a cylindrical vessel fitted with a frictionless piston. The gas is slowly heated for some time. During the process, 10 J of heat is supplied and the piston is found to move out 10 cm. Find the increase in the internal energy of the gas. The area of cross section of the cylinder = 4 cm2 and the atmospheric pressure = 100 kPa.
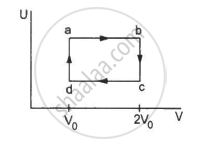
Figure shows the variation in the internal energy U with the volume V of 2.0 mol of an ideal gas in a cyclic process abcda. The temperatures of the gas at b and c are 500 K and 300 K respectively. Calculate the heat absorbed by the gas during the process.
Find the change in the internal energy of 2 kg of water as it is heated from 0°C to 4°C. The specific heat capacity of water is 4200 J kg−1 K−1 and its densities at 0°C and 4°C are 999.9 kg m−3 and 1000 kg m−3 respectively. Atmospheric pressure = 105 Pa.
An adiabatic vessel of total volume V is divided into two equal parts by a conducting separator. The separator is fixed in this position. The part on the left contains one mole of an ideal gas (U = 1.5 nRT) and the part on the right contains two moles of the same gas. Initially, the pressure on each side is p. The system is left for sufficient time so that a steady state is reached. Find (a) the work done by the gas in the left part during the process, (b) the temperature on the two sides in the beginning, (c) the final common temperature reached by the gases, (d) the heat given to the gas in the right part and (e) the increase in the internal energy of the gas in the left part.
Choose the correct option.
Which of the following is an example of the first law of thermodynamics?
A mixture of hydrogen and oxygen is enclosed in a rigid insulating cylinder. It is ignited by a spark. The temperature and pressure both increase considerably. Assume that the energy supplied by the spark is negligible, what conclusions may be drawn by application of the first law of thermodynamics?
For an Isothermal process
For an Isochoric process
Two moles of an ideal gas is expanded isothermally and reversibly at 300 K from 1 L to 10 L. The enthalpy change in kJ is ______.
Based on first law of thermodynamics which of the following is correct.
120 J of heat is added to a gaseous system, whose internal energy change is 60 J, then the amount of external work done is ____________.
An ideal gas undergoes cyclic process ABCDA as shown in given P-V diagram (figure). The amount of work done by the gas is ______.

Is it possible to increase the temperature of a gas without adding heat to it? Explain.
Consider a P-V diagram in which the path followed by one mole of perfect gas in a cylindrical container is shown in figure.
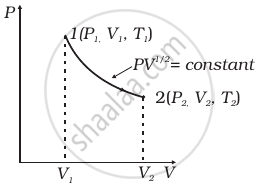
- Find the work done when the gas is taken from state 1 to state 2.
- What is the ratio of temperature T1/T2, if V2 = 2V1?
- Given the internal energy for one mole of gas at temperature T is (3/2) RT, find the heat supplied to the gas when it is taken from state 1 to 2, with V2 = 2V1.
Write the mathematical equation for the first law of thermodynamics for:
Isothermal process
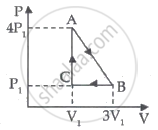
An ideal gas is taken through series of changes ABCA. The amount of work involved in the cycle is ______.
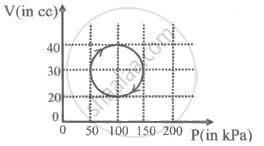
A system is taken through a cyclic process represented by a circle as shown. The heat absorbed by the system is ______.
An insulated container of gas has two chambers separated by an insulating partition. One of the chambers has volume V1 and contains ideal gas at pressure P1 and temperature T1. The other chamber has volume V2 and contains ideal gas at pressure P2 and temperature T2. If the partition is removed without doing any work on the gas, the final equilibrium temperature of the gas in the container will be ______.
Which among the following equations represents the first law of thermodynamics under isobaric conditions?
If one mole of monoatomic gas `(gamma=5/3)` is mixed with one mole of diatomic gas `(gamma=7/5)`, the value of γ for the mixture is ______.
A soap bubble in vacuum has a radius of 3 cm and another soap bubble in vacuum has a radius of 4 cm. If the two bubbles coalesce under isothermal condition, then the radius of the new bubble is ______.
ΔU = 0 is true for ______.
The amount of work done in increasing the voltage across the plates of capacitor from 5 V to 10 V is W. The work done in increasing it from 10 V to 15 V will be ______.
If the adiabatic ratio for a gas is 5/3, find the molar specific heat capacity of the gas at (i) constant volume (ii) constant pressure.
For an isothermal and reversible expansion of 0.5 mol of an ideal gas Wmax is - 3.918 kJ. The value of ΔU is ______.
Calculate work done when 2 moles of ideal gas expands by 5 dm3 isothermally at pressure 1.2 bar.
