Advertisements
Advertisements
Question
Consider a P-V diagram in which the path followed by one mole of perfect gas in a cylindrical container is shown in figure.
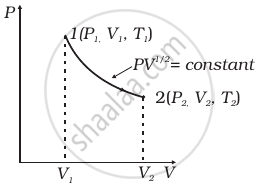
- Find the work done when the gas is taken from state 1 to state 2.
- What is the ratio of temperature T1/T2, if V2 = 2V1?
- Given the internal energy for one mole of gas at temperature T is (3/2) RT, find the heat supplied to the gas when it is taken from state 1 to 2, with V2 = 2V1.
Solution
Let `PV^(1/2) = K` = constant, `P = K/sqrt(V)`
Hence we can write, `P_1V_1^(1/2) = P_2V_2^(1/2) = K`
a. Work done for the process 1 to 2,
`W_(1 - > 2) int_(V_1)^(V_2) PdV`
= `int_(V_1)^(V_2) K/sqrt(V) dV`
= `K[sqrt(V)/(1/2)]_(V_1)^(V_2)`
= `2K(sqrt(V_2) - sqrt(V_1))`
= `2P_1V_1^(1/2) (sqrt(V_2) - sqrt(V_1))`
= `2P_2V_2^(1/2) (sqrt(V_2) - V_1)`
b. From the ideal gas equation,
`PV = nRT`
⇒ `T = (PV)/(nR)`
= `(Psqrt(V) sqrt(V))/(nR)`
⇒ `T = (Ksqrt(V))/(nR)` .....As, `P sqrt(V) = K`)
i.e., `T ∝ sqrt(V)`
Thus, `T_2/T_1 = sqrt(V^2/V_1)`
= `sqrt((2V_1)/V_1)`
= `sqrt(2)` .....(As V2 = 2V1)
c. Given, the internal energy of the gas, `U = (3/2) RT`
`ΔU = U_2 - U_1`
= `3/2 R(T_2 - T_1)`
= `3/2 R(sqrt(2)T_1 - T_1)`
= `3/2 RT_1(sqrt(2) - 1)` .....[∵ T2 = `sqrt(2)` T1 from (b)]
`ΔW = W_(1 -> 2)`
= `2P_1V_1^(1/2) (V_2^(1/2) - V_1^(1/2))`
= `2P_1V_1 (V_1^(1/2)/V_1^(1/2) - 1)`
= `2RT_1(sqrt(2) - 1)` ......`("As" P_1V_1 = RT_1 and V_2^(1/2)/V_1^(1/2) = sqrt(2))`
`ΔQ = ΔU + ΔW = 3/2 RT_1 (sqrt(2) - 1) + 2RT_1 (sqrt(2) - 1)`
= `7/2 RT_1 (sqrt(2) - 1)`
This is the amount of heat supplied.
APPEARS IN
RELATED QUESTIONS
50 cal of heat should be supplied to take a system from the state A to the state B through the path ACB as shown in figure. Find the quantity of heat to be suppled to take it from A to B via ADB.

The internal energy of a gas is given by U = 1.5 pV. It expands from 100 cm3 to 200 cm3against a constant pressure of 1.0 × 105 Pa. Calculate the heat absorbed by the gas in the process.
A gas is enclosed in a cylindrical vessel fitted with a frictionless piston. The gas is slowly heated for some time. During the process, 10 J of heat is supplied and the piston is found to move out 10 cm. Find the increase in the internal energy of the gas. The area of cross section of the cylinder = 4 cm2 and the atmospheric pressure = 100 kPa.
Answer the following in one or two sentences.
State the first law of thermodynamics.
When heat energy of 2000 joules is supplied to a gas at constant pressure 2.1 x 105 N/m2, there is an increase in its volume equal to 2.5 x 10-3 m3. The increase in internal energy of the gas in joules is ____________.
120 J of heat is added to a gaseous system, whose internal energy change is 60 J, then the amount of external work done is ____________.
Is it possible to increase the temperature of a gas without adding heat to it? Explain.
Consider that an ideal gas (n moles) is expanding in a process given by P = f(V), which passes through a point (V0, P0). Show that the gas is absorbing heat at (P0, V0) if the slope of the curve P = f(V) is larger than the slope of the adiabat passing through (P0, V0).
Define the isothermal process.
Define isochoric process
