Advertisements
Advertisements
प्रश्न
Consider a P-V diagram in which the path followed by one mole of perfect gas in a cylindrical container is shown in figure.
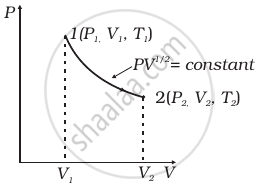
- Find the work done when the gas is taken from state 1 to state 2.
- What is the ratio of temperature T1/T2, if V2 = 2V1?
- Given the internal energy for one mole of gas at temperature T is (3/2) RT, find the heat supplied to the gas when it is taken from state 1 to 2, with V2 = 2V1.
उत्तर
Let `PV^(1/2) = K` = constant, `P = K/sqrt(V)`
Hence we can write, `P_1V_1^(1/2) = P_2V_2^(1/2) = K`
a. Work done for the process 1 to 2,
`W_(1 - > 2) int_(V_1)^(V_2) PdV`
= `int_(V_1)^(V_2) K/sqrt(V) dV`
= `K[sqrt(V)/(1/2)]_(V_1)^(V_2)`
= `2K(sqrt(V_2) - sqrt(V_1))`
= `2P_1V_1^(1/2) (sqrt(V_2) - sqrt(V_1))`
= `2P_2V_2^(1/2) (sqrt(V_2) - V_1)`
b. From the ideal gas equation,
`PV = nRT`
⇒ `T = (PV)/(nR)`
= `(Psqrt(V) sqrt(V))/(nR)`
⇒ `T = (Ksqrt(V))/(nR)` .....As, `P sqrt(V) = K`)
i.e., `T ∝ sqrt(V)`
Thus, `T_2/T_1 = sqrt(V^2/V_1)`
= `sqrt((2V_1)/V_1)`
= `sqrt(2)` .....(As V2 = 2V1)
c. Given, the internal energy of the gas, `U = (3/2) RT`
`ΔU = U_2 - U_1`
= `3/2 R(T_2 - T_1)`
= `3/2 R(sqrt(2)T_1 - T_1)`
= `3/2 RT_1(sqrt(2) - 1)` .....[∵ T2 = `sqrt(2)` T1 from (b)]
`ΔW = W_(1 -> 2)`
= `2P_1V_1^(1/2) (V_2^(1/2) - V_1^(1/2))`
= `2P_1V_1 (V_1^(1/2)/V_1^(1/2) - 1)`
= `2RT_1(sqrt(2) - 1)` ......`("As" P_1V_1 = RT_1 and V_2^(1/2)/V_1^(1/2) = sqrt(2))`
`ΔQ = ΔU + ΔW = 3/2 RT_1 (sqrt(2) - 1) + 2RT_1 (sqrt(2) - 1)`
= `7/2 RT_1 (sqrt(2) - 1)`
This is the amount of heat supplied.
APPEARS IN
संबंधित प्रश्न
The pressure of a gas changes linearly with volume from 10 kPa, 200 cc to 50 kPa, 50 cc. (a) Calculate the work done by the gas. (b) If no heat is supplied or extracted from the gas, what is the change in the internal energy of the gas?
ΔU is equal to ____________ work.
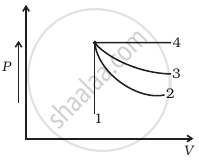
An ideal gas undergoes four different processes from the same initial state (figure). Four processes are adiabatic, isothermal, isobaric and isochoric. Out of 1, 2, 3 and 4 which one is adiabatic.
An ideal gas undergoes isothermal process from some initial state i to final state f. Choose the correct alternatives.
- dU = 0
- dQ= 0
- dQ = dU
- dQ = dW
The initial state of a certain gas is (Pi, Vi, Ti). It undergoes expansion till its volume becomes Vf. Consider the following two cases:
- the expansion takes place at constant temperature.
- the expansion takes place at constant pressure.
Plot the P-V diagram for each case. In which of the two cases, is the work done by the gas more?
Consider that an ideal gas (n moles) is expanding in a process given by P = f(V), which passes through a point (V0, P0). Show that the gas is absorbing heat at (P0, V0) if the slope of the curve P = f(V) is larger than the slope of the adiabat passing through (P0, V0).
Consider one mole of perfect gas in a cylinder of unit cross section with a piston attached (figure). A spring (spring constant k) is attached (unstretched length L) to the piston and to the bottom of the cylinder. Initially the spring is unstretched and the gas is in equilibrium. A certain amount of heat Q is supplied to the gas causing an increase of volume from V0 to V1.
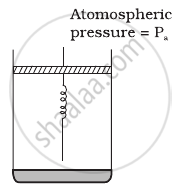
- What is the initial pressure of the system?
- What is the final pressure of the system?
- Using the first law of thermodynamics, write down a relation between Q, Pa, V, Vo and k.
For an isothermal and reversible expansion of 0.5 mol of an ideal gas Wmax is - 3.918 kJ. The value of ΔU is ______.
Obtain an expression for the workdone by a gas in an isothermal process.
What is an isothermal process?
