Advertisements
Advertisements
प्रश्न
A cycle followed by an engine (made of one mole of perfect gas in a cylinder with a piston) is shown in figure.
A to B : volume constant
B to C : adiabatic
C to D : volume constant
D to A : adiabatic
VC = VD = 2VA = 2VB
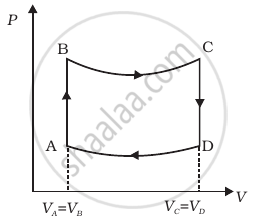
- In which part of the cycle heat is supplied to the engine from outside?
- In which part of the cycle heat is being given to the surrounding by the engine?
- What is the work done by the engine in one cycle? Write your answer in term of PA, PB, VA.
- What is the efficiency of the engine?
(γ = `5/3` for the gas), (Cv = `3/2` R for one mole)
उत्तर
a. For process AB (which is the isochoric process), volume is constant.
So, dV = 0
⇒ dW = 0
dQ = dU + dW = dU
⇒ dQ = dU = Change in internal energy
Hence, in this process heat supplied is utilised to increase, the internal energy of the system.
b. For the process CD (which is also an isochoric process), volume is constant but the pressure decreases. Hence, temperature also decreases (because PαT) so heat is given to the surroundings.
c. To calculate work done by the engine in one cycle, we calculate work done in each part separately.
(i) `W_(AB) = int_A^B PdV` = 0
(ii) `W_(CD) = int_C^D PdV` = 0 ....(As V is constant, dV = 0)
(iii) `W_(BC) = int_B^C PdV`
= `K int_B^C (dV)/(V^γ)`
= `K int_(V_B)^(V_C) V^-γ dV`
= `K/(1 - γ) [V^(1 - γ)]_(V_B)^(V_C)`
= `(K[V_C^(1 - γ) - V_B])/(1 - γ)` .....(PVγ = K for an adiabatic change)
= `([(P_CV_C^γ)(V_C^(1 - γ)) - (P_BV_B^γ)(V_B^(1 - γ))])/((1 - γ))`
Similarly, `W_(DA) = int_(V_D)^(V_A) PdV`
= `1/((1 - γ)) (P_AV_A - P_DV_D)` ......[∵ BC is an adiabatic process]
Since B and C lies on adiabatic curve BC,
∴ `P_BV_B^γ = P_CV_C^γ`
`P_C = P_B(V_B/V_C)^γ`
= `P_B(1/2)^γ`
= `2^(-γ)P_B`
Similarly, `P_D = 2^(-γ)P_A`
Total work done by the engine in one cycle ABCDA
`W = W_(AB) + W_(BC) + W_(CD) + W_(DA) = W_(BC) + W_(DA)`
= `((P_CV_C - P_BV_B))/(1 - γ) + ((P_AV_A - P_DV_D))/(1 - γ)`
`W = 1/(1 - γ) [2^(-γ) P_B (2V_B) - P_BV_B + P_AV_A - 2^(-γ) P_B (2V_B)]`
= `1/(1 - γ) [P_AV_B (2^(-γ + 1) - 1) - P_AV_A (2^(-γ + 1) - 1)`
= `1/(1 - γ) (2^(1 - γ) - 1) (P_B - P_A)V_A`
= `3/2 [1 - (1/2)^(2/3)](P_B - P_A)V_A`
d. Heat (Q) is supplied to the engine only from A to B. Thus Q = ΔQAB = ΔUAB = nCVΔT
= `3/2 R(T_B - T_A)` .....[As CV = (3/2)R and ΔT = TB – TA]
= `P_CV_C^γ = P_BV_B^γ`,
`P_C = P_B(V_B/V_C)^γ`
= `P_B(1/2)^γ`
= `P_B2^-γ` .....(As VB/VC = 1/2)
Thus, `P_CV_C^γ = (P_B2^-γ)(2V_B) = 2^(1 - γ)P_BV_B`
= `3/2 (P_BV_B - P_AV_A)`
= `3/2 (P_B - P_A)V_A` .....(PV = RT and VB = VA)
The efficiency of the engine,
η = `W/Q = (3/2 [1 - (1/2)^(2/3)] (P_B - P_A)V_A)/(3/2 (P_B - P_A)V_A)`
= `[1 - (1/2)^(2/3)]`
APPEARS IN
संबंधित प्रश्न
The first law of thermodynamics is a statement of ____________ .
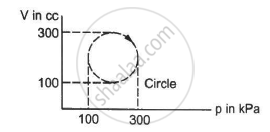
Calculate the heat absorbed by a system in going through the cyclic process shown in figure.
120 J of heat is added to a gaseous system, whose internal energy change is 60 J, then the amount of external work done is ____________.
For a particular reaction, the system absorbs 8 kJ of heat and does 2.5 kJ of work on its surrounding. What will be the change in internal energy of the system?
The isothermal bulk modulus of a perfect gas at pressure P is numerically equal to ____________.
An electric appliance supplies 6000 J/min heat to the system. If the system delivers a power of 90 W. How long it would take to increase the internal energy by 2.5 × 103 J?
An ideal gas having pressure p, volume V and temperature T undergoes a thermodynamic process in which dW = 0 and dQ < 0. Then, for the gas ______.
What is true for an adiabatic process?
Choose the correct relation with reason.
Obtain an expression for the workdone by a gas in an isothermal process.
