Advertisements
Advertisements
Question
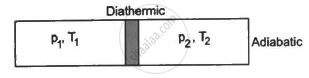
Figure shows a cylindrical tube of volume V with adiabatic walls containing an ideal gas. The internal energy of this ideal gas is given by 1.5 nRT. The tube is divided into two equal parts by a fixed diathermic wall. Initially, the pressure and the temperature are p1, T1 on the left and p2, T2 on the right. The system is left for sufficient time so that the temperature becomes equal on the two sides. (a) How much work has been done by the gas on the left part? (b) Find the final pressures on the two sides. (c) Find the final equilibrium temperature. (d) How much heat has flown from the gas on the right to the gas on the left?
Solution
Let n1 , U1 and n2 ,U2 be the no. of moles , internal energy of ideal gas in the left chamber and right chamber respectively.
(a) As the diathermic wall is fixed, so final volume of the chambers will be same. Thus, ΔV = 0, hence work done ΔW= P Δ V = 0
by eq. of state in the first and second chamber
`P_1V/2=n_1RT_1`
`rArr n_1=(P_1V)/(2RT_1)`
`P_2V/2=n_2RT_2`
`rArr n_2=(P_2V)/(2RT_2)`
n = n1 + n2
`rArrn=(P_1V)/(2RT_1)+(P_2V)/(2RT_2)=V/(2R)((P_1T_2+P_2T_1)/(T_1T_2))`
Again,
U = nCvT
`rArrnC_"v"T=1.5nRT`
`rArrC_"v"=1.5R`
In the first and second chamber internal energy is given by
U1 = n1CvT1 = n1 1.5RT1
U2 = n2CvT2 = n2 1.5RT2
U = U1 + U2
1.5nRT = n1 1.5RT1 + n2 1.5RT2
⇒ nT = n1T1 + n2T2
`rArrnT = (P_1V)/(2RT_1)T_1+(P-2V)/(2RT_2)T_2=((P_1+P_2)V)/(2R)`
`rArrT=((P_1+P_2)V)/(2nR)=((P_1+P_2)V)/(2RV/(2R)((P_1T_2+P_2T_1)/(T_1T_2)))=(T_1T_2(P_1+P_2))/(P_1T_2+P_2T_1)................(1)`
b) Let final pressure in the first and second compartment P1' and P2'.
By five variable equ of state in the first chamber
`(P_1V/2)/T_1=(P_1'V/2)/T`
`rArrP_1'=P_1/T_1T`
By eq. (1)
`rArrP_1'=P_1/T_1(T_1T_2(P_1+P_2))/(P_1T_2+P_2T_1)=(P_1T_2(P_1+P_2))/(P_1T_2+P_2T_1)`
Similarly,
`rArrP_1'=P_2/T_2T=(P_2T_1(P_1+P_2))/(P_1T_2+P_2T_1)`
c) Final temperature will be
`T=(T_1T_2(P_1+P_2))/(P_1T_2+P_2T_1).............\left(\text{by equation (1)}\right)`
d) Heat lost by right chamber will be
n2CvT2 - n2CvT
`=(P_2V)/(2RT_2)1.5RT_2-(P_2V)/(2RT_2)1.5R(T_1T_2(P_1+P_2))/(P_1T_2+P_2T_1)`
`=(3P_2V)/4-(3P_2V)/4(T_1(P_1+P_2))/(P_1T_2+P_2T_1)`
`=(3P_2V)/4[1-(T_1(P_1+P_2))/(P_1T_2+P_2T_1)]`
`=(3P_2V)/4[(P_1T_2+P_2T_1-T_1(P_1+P_2))/(P_1T_2+P_2T_1)]`
`=(3P_1P_2V)/4[(T_2-T_1)/(P_1T_2+P_2T_1)]`
APPEARS IN
RELATED QUESTIONS
A steam engine delivers 5.4×108 J of work per minute and services 3.6 × 109 J of heat per minute from its boiler. What is the efficiency of the engine? How much heat is wasted per minute?
The outer surface of a cylinder containing a gas is rubbed vigorously by a polishing machine. The cylinder and its gas become warm. Is the energy transferred to the gas heat or work?
When we rub our hands they become warm. Have we supplied heat to the hands?
An ideal gas is pumped into a rigid container having diathermic walls so that the temperature remains constant. In a certain time interval, the pressure in the container is doubled. Is the internal energy of the contents of the container also doubled in the interval ?
When a tyre bursts, the air coming out is cooler than the surrounding air. Explain.
Figure shows two processes A and B on a system. Let ∆Q1 and ∆Q2 be the heat given to the system in processes A and B respectively. Then ____________ .
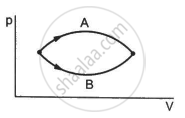
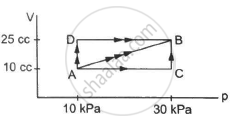
Figure shows three paths through which a gas can be taken from the state A to the state B. Calculate the work done by the gas in each of the three paths.
Explain given cases related to energy transfer between the system and surrounding –
- energy transferred (Q) > 0
- energy transferred (Q) < 0
- energy transferred (Q) = 0
In insulated systems, the amount of external work done by the gas is proportional to:
A person of mass 60 kg wants to lose 5kg by going up and down a 10 m high stairs. Assume he burns twice as much fat while going up than coming down. If 1 kg of fat is burnt on expending 7000 kilo calories, how many times must he go up and down to reduce his weight by 5 kg?
n mole of a perfect gas undergoes a cyclic process ABCA (see figure) consisting of the following processes:
A `→` B: Isothermal expansion at temperature T so that the volume is doubled from V1 to V2 = 2V1 and pressure changes from P1 to P2.
B `→` C: Isobaric compression at pressure P2 to initial volume V1.
C `→` A: Isochoric change leading to change of pressure from P2 to P1.
Total workdone in the complete cycle ABCA is ______.

A gas is compressed at a constant pressure of 50 N/m2 from a volume of 10 m3 to a volume of 4 m3. Energy of 100 J is then added to the gas by heating. Its internal energy is ______.
The internal energy of one mole of argon at 300 K is ______. (R = 8.314 J/mol.K)
The molar specific heat of He at constant volume is 12.47 J/mol.K. Two moles of He are heated at constant pressure. So the rise in temperature is 10 K. Find the increase in internal energy of the gas.
What is heat?
Explain the change in internal energy of a thermodynamic system (the gas) by heating it.
