Advertisements
Advertisements
Question
Figure shows three paths through which a gas can be taken from the state A to the state B. Calculate the work done by the gas in each of the three paths.
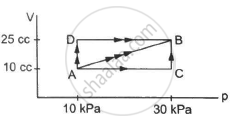
Solution
Work done during any process, W = P ∆ V
If both pressure and volume are changing during a process, then work done can be found out by finding the area under the PV diagram.
In path ACB, for line AC :-
Since initial volume is equal to final volume,
∆ V = 0
⇒ WAC = P ∆ V = 0
For line BC :-
P = 30 × 103 pa
WACB = WAC + WBC = 0 + P∆V
= 30 × 103 × (25 − 10) × 10−6
= 0.45 J
For path AB:-
Since both pressure and volume are changing, we use the mean pressure to find the work done.
Mean pressure, P = \[\frac{1}{2} \times (30 + 10) \times {10}^3\]
WAB = \[\frac{1}{2}\]× (10 + 30) × 103 × 15 × 10−6
= \[\frac{1}{2}\] × 40 × 15 × 10−3 = 0.30 J
Initial volume in path ADB, along line DB is the same as final volume. Thus, work done along this line is zero.
Along line AD, P = 10 kPa
W = WAD + WDB
= 10 × 103 (25 − 10) × 10−6 + 0
= 10 × 15 × 10−3 = 0.15 J
APPEARS IN
RELATED QUESTIONS
Two cylinders A and B of equal capacity are connected to each other via a stopcock. A contains a gas at standard temperature and pressure. B is completely evacuated. The entire system is thermally insulated. The stopcock is suddenly opened. Answer the following:
Do the intermediate states of the system (before settling to the final equilibrium state) lie on its P-V-T surface?
A force F is applied on a block of mass M. The block is displaced through a distance d in the direction of the force. What is the work done by the force on the block? Does the internal energy change because of this work?
The outer surface of a cylinder containing a gas is rubbed vigorously by a polishing machine. The cylinder and its gas become warm. Is the energy transferred to the gas heat or work?
Can work be done by a system without changing its volume?
A gas is contained in a metallic cylinder fitted with a piston. The piston is suddenly moved in to compress the gas and is maintained at this position. As time passes the pressure of the gas in the cylinder ______________ .
In a process on a system, the initial pressure and volume are equal to the final pressure and volume.
(a) The initial temperature must be equal to the final temperature.
(b) The initial internal energy must be equal to the final internal energy.
(c) The net heat given to the system in the process must be zero.
(d) The net work done by the system in the process must be zero.
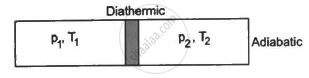
Figure shows a cylindrical tube of volume V with adiabatic walls containing an ideal gas. The internal energy of this ideal gas is given by 1.5 nRT. The tube is divided into two equal parts by a fixed diathermic wall. Initially, the pressure and the temperature are p1, T1 on the left and p2, T2 on the right. The system is left for sufficient time so that the temperature becomes equal on the two sides. (a) How much work has been done by the gas on the left part? (b) Find the final pressures on the two sides. (c) Find the final equilibrium temperature. (d) How much heat has flown from the gas on the right to the gas on the left?
A mixture of fuel and oxygen is burned in a constant-volume chamber surrounded by a water bath. It was noticed that the temperature of water is increased during the process. Treating the mixture of fuel and oxygen as the system,
- Has heat been transferred?
- Has work been done?
- What is the sign of ∆U?
What is the internal energy of the system, when the amount of heat Q is added to the system and the system does not do any work during the process?
A system releases 100 kJ of heat while 80 kJ of work is done on the system. Calculate the change in internal energy.
A cylinder containing one gram molecule of the gas was compressed adiabatically until its temperature rose from 27°C to 97°C. Calculate the work done and heat produced in the gas (𝛾 = 1.5).
Two samples A and B, of a gas at the same initial temperature and pressure are compressed from volume V to V/2; A isothermally and B adiabatically. The final pressure of A will be ______.
Two cylinders A and B of equal capacity are connected to each other via a stopcock. A contains a gas at standard temperature and pressure. B is completely evacuated. The entire system is thermally insulated. The stopcock is suddenly opened. Answer the following:
What is the final pressure of the gas in A and B?
Figure shows the P-V diagram of an ideal gas undergoing a change of state from A to B. Four different parts I, II, III and IV as shown in the figure may lead to the same change of state.

- Change in internal energy is same in IV and III cases, but not in I and II.
- Change in internal energy is same in all the four cases.
- Work done is maximum in case I
- Work done is minimum in case II.
n mole of a perfect gas undergoes a cyclic process ABCA (see figure) consisting of the following processes:
A `→` B: Isothermal expansion at temperature T so that the volume is doubled from V1 to V2 = 2V1 and pressure changes from P1 to P2.
B `→` C: Isobaric compression at pressure P2 to initial volume V1.
C `→` A: Isochoric change leading to change of pressure from P2 to P1.
Total workdone in the complete cycle ABCA is ______.

In thermodynamics, heat and work are ______.
An expansion process on a diatomic ideal gas (Cv = 5/2 R), has a linear path between the initial and final coordinates on a pV diagram. The coordinates of the initial state are: the pressure is 300 kPa, the volume is 0.08 m3 and the temperature is 390 K. The final pressure is 90 kPa and the final temperature s 320 K. The change in the internal energy of the gas, in SI units, is closest to:
The molar specific heat of He at constant volume is 12.47 J/mol.K. Two moles of He are heated at constant pressure. So the rise in temperature is 10 K. Find the increase in internal energy of the gas.
A steam engine delivers 4.8 x 108 Jof work per minute and services 1.2 x 109 J of heat per minute from its boiler. What is the percentage efficiency of the engine?
