Advertisements
Advertisements
Question
A system releases 100 kJ of heat while 80 kJ of work is done on the system. Calculate the change in internal energy.
Solution
Q = -100 kJ
W = -80 kJ
Q = ΔU + W
-100 = ΔU - 80
-100 + 80 = ΔU
ΔU = -20 kJ
APPEARS IN
RELATED QUESTIONS
In changing the state of a gas adiabatically from an equilibrium state A to another equilibrium state B, an amount of work equal to 22.3 J is done on the system. If the gas is taken from state A to B via a process in which the net heat absorbed by the system is 9.35 cal, how much is the net work done by the system in the latter case? (Take 1 cal = 4.19 J)
Two cylinders A and B of equal capacity are connected to each other via a stopcock. A contains a gas at standard temperature and pressure. B is completely evacuated. The entire system is thermally insulated. The stopcock is suddenly opened. Answer the following:
Do the intermediate states of the system (before settling to the final equilibrium state) lie on its P-V-T surface?
Should the internal energy of a system necessarily increase if heat is added to it?
A cylinder containing a gas is lifted from the first floor to the second floor. What is the amount of work done on the gas? What is the amount of work done by the gas? Is the internal energy of the gas increased? Is the temperature of the gas increased?
When we rub our hands they become warm. Have we supplied heat to the hands?
The final volume of a system is equal to the initial volume in a certain process. Is the work done by the system necessarily zero? Is it necessarily nonzero?
Can work be done by a system without changing its volume?
When a tyre bursts, the air coming out is cooler than the surrounding air. Explain.
Refer to figure. Let ∆U1 and ∆U2 be the changes in internal energy of the system in the process A and B. Then _____________ .

Consider the process on a system shown in figure. During the process, the work done by the system ______________ .
The pressure p and volume V of an ideal gas both increase in a process.
(a) Such a process is not possible.
(b) The work done by the system is positive.
(c) The temperature of the system must increase.
(d) Heat supplied to the gas is equal to the change in internal energy.
A 100 kg lock is started with a speed of 2.0 m s−1 on a long, rough belt kept fixed in a horizontal position. The coefficient of kinetic friction between the block and the belt is 0.20. (a) Calculate the change in the internal energy of the block-belt system as the block comes to a stop on the belt. (b) Consider the situation from a frame of reference moving at 2.0 m s−1 along the initial velocity of the block. As seen from this frame, the block is gently put on a moving belt and in due time the block starts moving with the belt at 2.0 m s−1. calculate the increase in the kinetic energy of the block as it stops slipping past the belt. (c) Find the work done in this frame by the external force holding the belt.
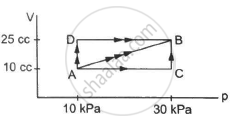
Figure shows three paths through which a gas can be taken from the state A to the state B. Calculate the work done by the gas in each of the three paths.
A gas is taken along the path AB as shown in figure. If 70 cal of heat is extracted from the gas in the process, calculate the change in the internal energy of the system.
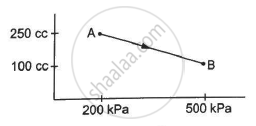
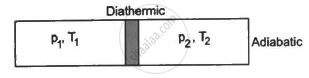
Figure shows a cylindrical tube of volume V with adiabatic walls containing an ideal gas. The internal energy of this ideal gas is given by 1.5 nRT. The tube is divided into two equal parts by a fixed diathermic wall. Initially, the pressure and the temperature are p1, T1 on the left and p2, T2 on the right. The system is left for sufficient time so that the temperature becomes equal on the two sides. (a) How much work has been done by the gas on the left part? (b) Find the final pressures on the two sides. (c) Find the final equilibrium temperature. (d) How much heat has flown from the gas on the right to the gas on the left?
A mixture of fuel and oxygen is burned in a constant-volume chamber surrounded by a water bath. It was noticed that the temperature of water is increased during the process. Treating the mixture of fuel and oxygen as the system,
- Has heat been transferred?
- Has work been done?
- What is the sign of ∆U?
Which of the following is correct, when the energy is transferred to a system from its environment?
When does a system lose energy to its surroundings and its internal energy decreases?
Explain the different ways through which the internal energy of the system can be changed.
A cylinder containing one gram molecule of the gas was compressed adiabatically until its temperature rose from 27°C to 97°C. Calculate the work done and heat produced in the gas (𝛾 = 1.5).
An ideal gas is compressed at a constant temperature. Its internal energy will ____________.
When 1 g of water at 0° C and 1 x 105 N/m2 pressure is converted into ice of volume 1.082 cm3, the external work done will be ____________.
Two cylinders A and B of equal capacity are connected to each other via a stopcock. A contains a gas at standard temperature and pressure. B is completely evacuated. The entire system is thermally insulated. The stopcock is suddenly opened. Answer the following:
What is the change in internal energy of the gas?
Figure shows the P-V diagram of an ideal gas undergoing a change of state from A to B. Four different parts I, II, III and IV as shown in the figure may lead to the same change of state.

- Change in internal energy is same in IV and III cases, but not in I and II.
- Change in internal energy is same in all the four cases.
- Work done is maximum in case I
- Work done is minimum in case II.
An expansion process on a diatomic ideal gas (Cv = 5/2 R), has a linear path between the initial and final coordinates on a pV diagram. The coordinates of the initial state are: the pressure is 300 kPa, the volume is 0.08 m3 and the temperature is 390 K. The final pressure is 90 kPa and the final temperature s 320 K. The change in the internal energy of the gas, in SI units, is closest to:
A gas is compressed at a constant pressure of 50 N/m2 from a volume of 10 m3 to a volume of 4 m3. Energy of 100 J is then added to the gas by heating. Its internal energy is ______.
A steam engine delivers 4.8 x 108 Jof work per minute and services 1.2 x 109 J of heat per minute from its boiler. What is the percentage efficiency of the engine?
What is heat?
Explain the change in internal energy of a thermodynamic system (the gas) by heating it.
