Advertisements
Advertisements
Question
What is the internal energy of the system, when the amount of heat Q is added to the system and the system does not do any work during the process?
Solution
The first law of thermodynamics is one of the most useful equations when dealing with internal energy, and it states that the change in internal energy of a system equals the heat added to the system minus the work done by the system.
∆U = Q − W
APPEARS IN
RELATED QUESTIONS
Explain why Two bodies at different temperatures T1 and T2, if brought in thermal contact, do not necessarily settle to the mean temperature (T1 + T2)/2.
In changing the state of a gas adiabatically from an equilibrium state A to another equilibrium state B, an amount of work equal to 22.3 J is done on the system. If the gas is taken from state A to B via a process in which the net heat absorbed by the system is 9.35 cal, how much is the net work done by the system in the latter case? (Take 1 cal = 4.19 J)
Two cylinders A and B of equal capacity are connected to each other via a stopcock. A contains a gas at standard temperature and pressure. B is completely evacuated. The entire system is thermally insulated. The stopcock is suddenly opened. Answer the following:
Do the intermediate states of the system (before settling to the final equilibrium state) lie on its P-V-T surface?
A cylinder containing a gas is lifted from the first floor to the second floor. What is the amount of work done on the gas? What is the amount of work done by the gas? Is the internal energy of the gas increased? Is the temperature of the gas increased?
The outer surface of a cylinder containing a gas is rubbed vigorously by a polishing machine. The cylinder and its gas become warm. Is the energy transferred to the gas heat or work?
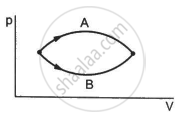
Figure shows two processes A and B on a system. Let ∆Q1 and ∆Q2 be the heat given to the system in processes A and B respectively. Then ____________ .
A gas is contained in a metallic cylinder fitted with a piston. The piston is suddenly moved in to compress the gas and is maintained at this position. As time passes the pressure of the gas in the cylinder ______________ .
The pressure p and volume V of an ideal gas both increase in a process.
(a) Such a process is not possible.
(b) The work done by the system is positive.
(c) The temperature of the system must increase.
(d) Heat supplied to the gas is equal to the change in internal energy.
A 100 kg lock is started with a speed of 2.0 m s−1 on a long, rough belt kept fixed in a horizontal position. The coefficient of kinetic friction between the block and the belt is 0.20. (a) Calculate the change in the internal energy of the block-belt system as the block comes to a stop on the belt. (b) Consider the situation from a frame of reference moving at 2.0 m s−1 along the initial velocity of the block. As seen from this frame, the block is gently put on a moving belt and in due time the block starts moving with the belt at 2.0 m s−1. calculate the increase in the kinetic energy of the block as it stops slipping past the belt. (c) Find the work done in this frame by the external force holding the belt.
A gas is taken through a cyclic process ABCA as shown in figure. If 2.4 cal of heat is given in the process, what is the value of J ?
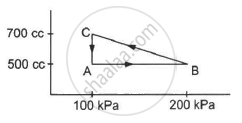
A gas is taken along the path AB as shown in figure. If 70 cal of heat is extracted from the gas in the process, calculate the change in the internal energy of the system.
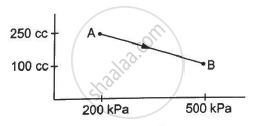
A gas is initially at a pressure of 100 kPa and its volume is 2.0 m3. Its pressure is kept constant and the volume is changed from 2.0 m3 to 2.5 m3. Its Volume is now kept constant and the pressure is increased from 100 kPa to 200 kPa. The gas is brought back to its initial state, the pressure varying linearly with its volume. (a) Whether the heat is supplied to or extracted from the gas in the complete cycle? (b) How much heat was supplied or extracted?
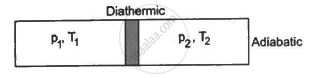
Figure shows a cylindrical tube of volume V with adiabatic walls containing an ideal gas. The internal energy of this ideal gas is given by 1.5 nRT. The tube is divided into two equal parts by a fixed diathermic wall. Initially, the pressure and the temperature are p1, T1 on the left and p2, T2 on the right. The system is left for sufficient time so that the temperature becomes equal on the two sides. (a) How much work has been done by the gas on the left part? (b) Find the final pressures on the two sides. (c) Find the final equilibrium temperature. (d) How much heat has flown from the gas on the right to the gas on the left?
A system releases 130 kJ of heat while 109 kJ of work is done on the system. Calculate the change in internal energy.
What is the energy associated with the random, disordered motion of the molecules of a system called as?
When does a system lose energy to its surroundings and its internal energy decreases?
Explain the different ways through which the internal energy of the system can be changed.
A cylinder containing one gram molecule of the gas was compressed adiabatically until its temperature rose from 27°C to 97°C. Calculate the work done and heat produced in the gas (𝛾 = 1.5).
When 1 g of water at 0° C and 1 x 105 N/m2 pressure is converted into ice of volume 1.082 cm3, the external work done will be ____________.
Two cylinders A and B of equal capacity are connected to each other via a stopcock. A contains a gas at standard temperature and pressure. B is completely evacuated. The entire system is thermally insulated. The stopcock is suddenly opened. Answer the following:
What is the final pressure of the gas in A and B?
In insulated systems, the amount of external work done by the gas is proportional to:
Figure shows the P-V diagram of an ideal gas undergoing a change of state from A to B. Four different parts I, II, III and IV as shown in the figure may lead to the same change of state.

- Change in internal energy is same in IV and III cases, but not in I and II.
- Change in internal energy is same in all the four cases.
- Work done is maximum in case I
- Work done is minimum in case II.
A person of mass 60 kg wants to lose 5kg by going up and down a 10 m high stairs. Assume he burns twice as much fat while going up than coming down. If 1 kg of fat is burnt on expending 7000 kilo calories, how many times must he go up and down to reduce his weight by 5 kg?
If a gas is compressed adiabatically:
The internal energy of one mole of argon at 300 K is ______. (R = 8.314 J/mol.K)
What is heat?
