Advertisements
Advertisements
प्रश्न
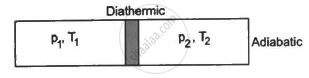
Figure shows a cylindrical tube of volume V with adiabatic walls containing an ideal gas. The internal energy of this ideal gas is given by 1.5 nRT. The tube is divided into two equal parts by a fixed diathermic wall. Initially, the pressure and the temperature are p1, T1 on the left and p2, T2 on the right. The system is left for sufficient time so that the temperature becomes equal on the two sides. (a) How much work has been done by the gas on the left part? (b) Find the final pressures on the two sides. (c) Find the final equilibrium temperature. (d) How much heat has flown from the gas on the right to the gas on the left?
उत्तर
Let n1 , U1 and n2 ,U2 be the no. of moles , internal energy of ideal gas in the left chamber and right chamber respectively.
(a) As the diathermic wall is fixed, so final volume of the chambers will be same. Thus, ΔV = 0, hence work done ΔW= P Δ V = 0
by eq. of state in the first and second chamber
`P_1V/2=n_1RT_1`
`rArr n_1=(P_1V)/(2RT_1)`
`P_2V/2=n_2RT_2`
`rArr n_2=(P_2V)/(2RT_2)`
n = n1 + n2
`rArrn=(P_1V)/(2RT_1)+(P_2V)/(2RT_2)=V/(2R)((P_1T_2+P_2T_1)/(T_1T_2))`
Again,
U = nCvT
`rArrnC_"v"T=1.5nRT`
`rArrC_"v"=1.5R`
In the first and second chamber internal energy is given by
U1 = n1CvT1 = n1 1.5RT1
U2 = n2CvT2 = n2 1.5RT2
U = U1 + U2
1.5nRT = n1 1.5RT1 + n2 1.5RT2
⇒ nT = n1T1 + n2T2
`rArrnT = (P_1V)/(2RT_1)T_1+(P-2V)/(2RT_2)T_2=((P_1+P_2)V)/(2R)`
`rArrT=((P_1+P_2)V)/(2nR)=((P_1+P_2)V)/(2RV/(2R)((P_1T_2+P_2T_1)/(T_1T_2)))=(T_1T_2(P_1+P_2))/(P_1T_2+P_2T_1)................(1)`
b) Let final pressure in the first and second compartment P1' and P2'.
By five variable equ of state in the first chamber
`(P_1V/2)/T_1=(P_1'V/2)/T`
`rArrP_1'=P_1/T_1T`
By eq. (1)
`rArrP_1'=P_1/T_1(T_1T_2(P_1+P_2))/(P_1T_2+P_2T_1)=(P_1T_2(P_1+P_2))/(P_1T_2+P_2T_1)`
Similarly,
`rArrP_1'=P_2/T_2T=(P_2T_1(P_1+P_2))/(P_1T_2+P_2T_1)`
c) Final temperature will be
`T=(T_1T_2(P_1+P_2))/(P_1T_2+P_2T_1).............\left(\text{by equation (1)}\right)`
d) Heat lost by right chamber will be
n2CvT2 - n2CvT
`=(P_2V)/(2RT_2)1.5RT_2-(P_2V)/(2RT_2)1.5R(T_1T_2(P_1+P_2))/(P_1T_2+P_2T_1)`
`=(3P_2V)/4-(3P_2V)/4(T_1(P_1+P_2))/(P_1T_2+P_2T_1)`
`=(3P_2V)/4[1-(T_1(P_1+P_2))/(P_1T_2+P_2T_1)]`
`=(3P_2V)/4[(P_1T_2+P_2T_1-T_1(P_1+P_2))/(P_1T_2+P_2T_1)]`
`=(3P_1P_2V)/4[(T_2-T_1)/(P_1T_2+P_2T_1)]`
APPEARS IN
संबंधित प्रश्न
Explain why Air pressure in a car tyre increases during driving.
Should the internal energy of a system necessarily increase if heat is added to it?
A cylinder containing a gas is lifted from the first floor to the second floor. What is the amount of work done on the gas? What is the amount of work done by the gas? Is the internal energy of the gas increased? Is the temperature of the gas increased?
An ideal gas goes from the state i to the state f as shown in figure. The work done by the gas during the process ______________ .
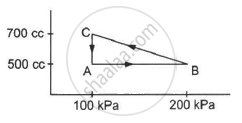
A gas is taken through a cyclic process ABCA as shown in figure. If 2.4 cal of heat is given in the process, what is the value of J ?
Which of the following system freely allows the exchange of energy and matter with its environment?
What is the internal energy of the system, when the amount of heat Q is added to the system and the system does not do any work during the process?
When does a system lose energy to its surroundings and its internal energy decreases?
A thermodynamic system goes from states
(i) P, V to 2P, V (ii) P, V to P, 2V
The work done in the two cases is ____________.
In a thermodynamic system, working substance is ideal gas. Its internal energy is in the form of ______.
When 1 g of water at 0° C and 1 x 105 N/m2 pressure is converted into ice of volume 1.082 cm3, the external work done will be ____________.
Two samples A and B, of a gas at the same initial temperature and pressure are compressed from volume V to V/2; A isothermally and B adiabatically. The final pressure of A will be ______.
Two cylinders A and B of equal capacity are connected to each other via a stopcock. A contains a gas at standard temperature and pressure. B is completely evacuated. The entire system is thermally insulated. The stopcock is suddenly opened. Answer the following:
What is the final pressure of the gas in A and B?
Two cylinders A and B of equal capacity are connected to each other via a stopcock. A contains a gas at standard temperature and pressure. B is completely evacuated. The entire system is thermally insulated. The stopcock is suddenly opened. Answer the following:
What is the change in the temperature of the gas?
In insulated systems, the amount of external work done by the gas is proportional to:
Figure shows the P-V diagram of an ideal gas undergoing a change of state from A to B. Four different parts I, II, III and IV as shown in the figure may lead to the same change of state.

- Change in internal energy is same in IV and III cases, but not in I and II.
- Change in internal energy is same in all the four cases.
- Work done is maximum in case I
- Work done is minimum in case II.
A person of mass 60 kg wants to lose 5kg by going up and down a 10 m high stairs. Assume he burns twice as much fat while going up than coming down. If 1 kg of fat is burnt on expending 7000 kilo calories, how many times must he go up and down to reduce his weight by 5 kg?
The molar specific heat of He at constant volume is 12.47 J/mol.K. Two moles of He are heated at constant pressure. So the rise in temperature is 10 K. Find the increase in internal energy of the gas.
What is heat?
A system releases 125 kJ of heat while 104 kJ work is done on the system. Calculate the change in internal energy.
