Question

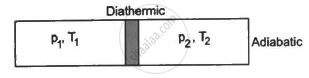
Figure shows a cylindrical tube of volume V with adiabatic walls containing an ideal gas. The internal energy of this ideal gas is given by 1.5 nRT. The tube is divided into two equal parts by a fixed diathermic wall. Initially, the pressure and the temperature are p₁, T₁ on the left and p₂, T₂ on the right. The system is left for sufficient time so that the temperature becomes equal on the two sides. (a) How much work has been done by the gas on the left part? (b) Find the final pressures on the two sides. (c) Find the final equilibrium temperature. (d) How much heat has flown from the gas on the right to the gas on the left?

Answer 1

Let n₁ , U₁ and n₂ ,U₂ be the no. of moles , internal energy of ideal gas in the left chamber and right chamber respectively.

(a) As the diathermic wall is fixed, so final volume of the chambers will be same. Thus, ΔV = 0, hence work done ΔW= P Δ V = 0

by eq. of state in the first and second chamber

`P_1V/2=n_1RT_1`

`rArr n_1=(P_1V)/(2RT_1)`

`P_2V/2=n_2RT_2`

`rArr n_2=(P_2V)/(2RT_2)`

n = n₁ + n₂

`rArrn=(P_1V)/(2RT_1)+(P_2V)/(2RT_2)=V/(2R)((P_1T_2+P_2T_1)/(T_1T_2))`

Again,

U = nC_vT

`rArrnC_"v"T=1.5nRT`

`rArrC_"v"=1.5R`

In the first and second chamber internal energy is given by

U₁ = n₁C_vT₁ = n₁ 1.5RT₁

U₂ = n₂C_vT₂ = n₂ 1.5RT₂

U = U₁ + U₂

1.5nRT = n₁ 1.5RT₁ + n₂ 1.5RT₂

⇒ nT = n₁T₁ + n₂T₂

`rArrnT = (P_1V)/(2RT_1)T_1+(P-2V)/(2RT_2)T_2=((P_1+P_2)V)/(2R)`

`rArrT=((P_1+P_2)V)/(2nR)=((P_1+P_2)V)/(2RV/(2R)((P_1T_2+P_2T_1)/(T_1T_2)))=(T_1T_2(P_1+P_2))/(P_1T_2+P_2T_1)................(1)`

b) Let final pressure in the first and second compartment P₁' and P₂'.

By five variable equ of state in the first chamber

`(P_1V/2)/T_1=(P_1'V/2)/T`

`rArrP_1'=P_1/T_1T`

By eq. (1)

`rArrP_1'=P_1/T_1(T_1T_2(P_1+P_2))/(P_1T_2+P_2T_1)=(P_1T_2(P_1+P_2))/(P_1T_2+P_2T_1)`

Similarly,

`rArrP_1'=P_2/T_2T=(P_2T_1(P_1+P_2))/(P_1T_2+P_2T_1)`

c) Final temperature will be

`T=(T_1T_2(P_1+P_2))/(P_1T_2+P_2T_1).............\left(\text{by equation (1)}\right)`

d) Heat lost by right chamber will be

n₂C_vT₂ - n₂C_vT

`=(P_2V)/(2RT_2)1.5RT_2-(P_2V)/(2RT_2)1.5R(T_1T_2(P_1+P_2))/(P_1T_2+P_2T_1)`

`=(3P_2V)/4-(3P_2V)/4(T_1(P_1+P_2))/(P_1T_2+P_2T_1)`

`=(3P_2V)/4[1-(T_1(P_1+P_2))/(P_1T_2+P_2T_1)]`

`=(3P_2V)/4[(P_1T_2+P_2T_1-T_1(P_1+P_2))/(P_1T_2+P_2T_1)]`

`=(3P_1P_2V)/4[(T_2-T_1)/(P_1T_2+P_2T_1)]`