Advertisements
Advertisements
प्रश्न
Consider two containers A and B containing identical gases at the same pressure, volume and temperature. The gas in container A is compressed to half of its original volume isothermally while the gas in container B is compressed to half of its original value adiabatically. The ratio of final pressure of gas in B to that of gas in A is ______.
विकल्प
`2^(γ - 1)`
`(1/2)^(γ - 1)`
`(1/(1 - γ))^2`
`(1/(γ - 1))^2`
उत्तर
Consider two containers A and B containing identical gases at the same pressure, volume and temperature. The gas in container A is compressed to half of its original volume isothermally while the gas in container B is compressed to half of its original value adiabatically. The ratio of final pressure of gas in B to that of gas in A is `underline(2^(γ - 1))`.
Explanation:
According to the P-V diagram is shown for container A (which is going through an isothermal process) and for container B (which is going through an adiabatic process).
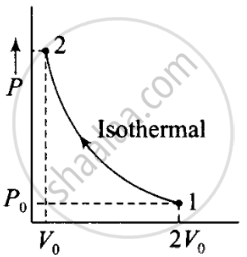
V →container A

V →container A
Both processes involve compression of the gas.
(i) Isothermal compression (gas A) (during 1→ 2)
P1V1 = P2V2
⇒ P0(2V0)γ = P2(V0)γ
⇒ P0(2V0) = P2(V0)
(ii) Adiabatic compression, (gas B) (during 1→ 2)
P1V1γ = P2V2γ
⇒ P0(2V0)γ = P2(V0)γ
⇒ P2 = `((2V_0)/V_0) P_0 - (2)^γ P_0`
Hence `((P_2)_B)/((P_2)_A)` = ratio of final pressure = `((2)^γ P_0)/(2P_0) = 2^(γ - 1)` where, γ is ratio of specific heat capacities for the gas.
APPEARS IN
संबंधित प्रश्न
When we heat an object, it expands. Is work done by the object in this process? Is heat given to the object equal to the increase in its internal energy?
The pressure of a gas changes linearly with volume from 10 kPa, 200 cc to 50 kPa, 50 cc. (a) Calculate the work done by the gas. (b) If no heat is supplied or extracted from the gas, what is the change in the internal energy of the gas?
The internal energy of a gas is given by U = 1.5 pV. It expands from 100 cm3 to 200 cm3against a constant pressure of 1.0 × 105 Pa. Calculate the heat absorbed by the gas in the process.
An adiabatic vessel of total volume V is divided into two equal parts by a conducting separator. The separator is fixed in this position. The part on the left contains one mole of an ideal gas (U = 1.5 nRT) and the part on the right contains two moles of the same gas. Initially, the pressure on each side is p. The system is left for sufficient time so that a steady state is reached. Find (a) the work done by the gas in the left part during the process, (b) the temperature on the two sides in the beginning, (c) the final common temperature reached by the gases, (d) the heat given to the gas in the right part and (e) the increase in the internal energy of the gas in the left part.
10 kg of four different gases (Cl2, CH4, O2, N2) expand isothermally and reversibly from 20 atm to 10 atm. The order of amount of work will be ____________.
An ideal gas undergoes isothermal process from some initial state i to final state f. Choose the correct alternatives.
- dU = 0
- dQ= 0
- dQ = dU
- dQ = dW
Consider that an ideal gas (n moles) is expanding in a process given by P = f(V), which passes through a point (V0, P0). Show that the gas is absorbing heat at (P0, V0) if the slope of the curve P = f(V) is larger than the slope of the adiabat passing through (P0, V0).
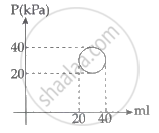
In the reported figure, heat energy absorbed by a system in going through a cyclic process is ______ πJ.
Using the first law of thermodynamics, show that for an ideal gas, the difference between the molar specific heat capacities at constant pressure and at constant volume is equal to the molar gas constant R.
Calculate work done when 2 moles of ideal gas expands by 5 dm3 isothermally at pressure 1.2 bar.
