Advertisements
Advertisements
Question
An electron in an atom is revolving round the nucleus in a circular orbit of radius 5.3 × 10-11 m with a speed of 3 × 106 m/s. Find the angular momentum of electron.
Solution
Given,
r = 5.3 × 10-11 m
v = 3 × 106 m/s
m = 9.1 × 10-31 kg
L = ?
Angular momentum of electron is
L = m v r
= 9.1 × 10-31 × 3 × 106 × 5.3 × 10-11
= 1.447 × 10-34 kg m2/s
∴ Angular momentum of electron is 1.447 × 10-34 kg m2/s.
APPEARS IN
RELATED QUESTIONS
State the law of conservation of angular momentum and explain with a suitable example.
Obtain an expression for the torque acting on a rotating body with constant angular acceleration. Hence state the dimensions and SI unit of torque.
Define moment of inertia. State its SI unit and dimensions.
A flywheel is revolving with a constant angular velocity. A chip of its rim breaks and flies away. What will be the effect on its angular velocity?
An electron(e) is revolving in a circular orbit of radius r in the hydrogen atom. The angular momentum of the electron is (M = magnetic dipole moment associated with it and m = mass of electron)
A stone of mass 1 kg is rotated in a horizontal circle of radius 0.5 m. If it makes `100/pi` rps, then its angular momentum is ______
A charged particle (charge = q: mass = m) is rotating in a circle of radius 'R' with uniform speed 'v'. The ratio of its magnetic moment (M) to the angular momentum (L) is ______
If the angular momentum of a body increases by 50%, then its kinetic energy of rotation increases by ______ (M.I. remains constant)
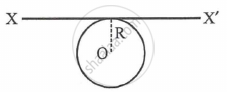
A thin metal wire of length 'L' and uniform linear mass density 'ρ' is bent into a circular coil with 'O' as centre. The moment of inertia of a coil about the axis XX' is ______.
If the angular momentum of an electron is `vec"J"` then the magnitude of the magnetic moment will be ____________.
Let I1 and I2 be the moments of inertia of two bodies of identical geometrical shape. If the first body is made of aluminium and the second of iron, then ____________.
An electron has a mass of 9.1 x 10-31 kg. It revolves round the nucleus in a circular orbit of radius 0.529 x 10-10 metre at a speed of 2.2 x 106 m/s. The magnitude of its linear momentum in this motion is ____________.
A particle is revolving in anticlockwise sense along the circumference of a circle of radius 'r' with linear velocity 'v', then the angle between 'v' and angular velocity 'ω' will be ______.
Three-point masses each of mass 'M' are placed at the corners of an equilateral triangle of side 'a'. The moment of inertia of this system about an axis passing through one side of a triangle is ______.
A wheel of moment of inertia 2 kg m2 is rotating about an axis passing through centre and perpendicular to its plane at a speed 60 rad/s. Due to friction, it comes to rest in 5 minutes. The angular momentum of the wheel three minutes before it stops rotating is ______.
A disc of moment of inertia 'I1' is rotating in horizontal plane about an axis passing through a centre and perpendicular to its plane with constant angular speed 'ω1'. Another disc of moment of inertia 'I2' having zero angular speed is placed co-axially on a rotating disc. Now, both the discs are rotating with constant angular speed 'ω2'. The energy lost by the initial rotating disc is ______.
A particle of mass m = 5 unit is moving with a uniform speed v = 3`sqrt2` unit in the XY-plane along the line y = x + 4. The magnitude of the angular momentum about origin is ______.
The difference in the angular momentum of an electron in two successive orbits of a hydrogen atom is ______.
The angular momentum of the electron in the second orbit of hydrogen atom is L. The angular momentum in the third orbit is ______.
Define moment of inertia.
Define angular momentum.
