Advertisements
Advertisements
Question
As one considers orbits with higher values of n in a hydrogen atom, the electric potential energy of the atom
Options
decreases
increases
remains the same
does not increase
Solution
increases
The electric potential energy of hydrogen atom with electron at the nth state is given by
V = - `(2xx13.6)/n^2`
As the value of n increases, the potential energy of the hydrogen atom also increases, i.e. the atom becomes less bound as n increases.
APPEARS IN
RELATED QUESTIONS
When white radiation is passed through a sample of hydrogen gas at room temperature, absorption lines are observed in Lyman series only. Explain.
The minimum orbital angular momentum of the electron in a hydrogen atom is
In which of the following systems will the radius of the first orbit (n = 1) be minimum?
Which of the following curves may represent the speed of the electron in a hydrogen atom as a function of trincipal quantum number n?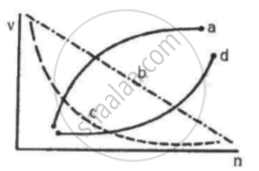
The radius of the shortest orbit in a one-electron system is 18 pm. It may be
An electron with kinetic energy 5 eV is incident on a hydrogen atom in its ground state. The collision
Let An be the area enclosed by the nth orbit in a hydrogen atom. The graph of ln (An/A1) against ln(n)
(a) will pass through the origin
(b) will be a straight line with slope 4
(c) will be a monotonically increasing nonlinear curve
(d) will be a circle
Find the binding energy of a hydrogen atom in the state n = 2.
(a) Find the first excitation potential of He+ ion. (b) Find the ionization potential of Li++ion.
A hydrogen atom in a state having a binding energy of 0.85 eV makes transition to a state with excitation energy 10.2 e.V (a) Identify the quantum numbers n of the upper and the lower energy states involved in the transition. (b) Find the wavelength of the emitted radiation.
What is the energy of a hydrogen atom in the first excited state if the potential energy is taken to be zero in the ground state?
A gas of hydrogen-like ions is prepared in a particular excited state A. It emits photons having wavelength equal to the wavelength of the first line of the Lyman series together with photons of five other wavelengths. Identify the gas and find the principal quantum number of the state A.
Find the maximum angular speed of the electron of a hydrogen atom in a stationary orbit.
Suppose, in certain conditions only those transitions are allowed to hydrogen atoms in which the principal quantum number n changes by 2. (a) Find the smallest wavelength emitted by hydrogen. (b) List the wavelength emitted by hydrogen in the visible range (380 nm to 780 nm).
Electrons are emitted from an electron gun at almost zero velocity and are accelerated by an electric field E through a distance of 1.0 m. The electrons are now scattered by an atomic hydrogen sample in ground state. What should be the minimum value of E so that red light of wavelength 656.3 nm may be emitted by the hydrogen?
A hydrogen atom moving at speed υ collides with another hydrogen atom kept at rest. Find the minimum value of υ for which one of the atoms may get ionized.
The mass of a hydrogen atom = 1.67 × 10−27 kg.
When a photon is emitted from an atom, the atom recoils. The kinetic energy of recoil and the energy of the photon come from the difference in energies between the states involved in the transition. Suppose, a hydrogen atom changes its state from n = 3 to n = 2. Calculate the fractional change in the wavelength of light emitted, due to the recoil.
In a hydrogen atom the electron moves in an orbit of radius 0.5 A° making 10 revolutions per second, the magnetic moment associated with the orbital motion of the electron will be ______.
The Balmer series for the H-atom can be observed ______.
- if we measure the frequencies of light emitted when an excited atom falls to the ground state.
- if we measure the frequencies of light emitted due to transitions between excited states and the first excited state.
- in any transition in a H-atom.
- as a sequence of frequencies with the higher frequencies getting closely packed.
Let En = `(-1)/(8ε_0^2) (me^4)/(n^2h^2)` be the energy of the nth level of H-atom. If all the H-atoms are in the ground state and radiation of frequency (E2 - E1)/h falls on it ______.
- it will not be absorbed at all.
- some of atoms will move to the first excited state.
- all atoms will be excited to the n = 2 state.
- no atoms will make a transition to the n = 3 state.
