Advertisements
Advertisements
Question
Attempt this question on graph paper.
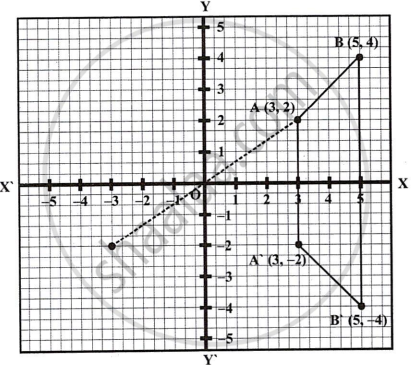
- Plot A (3, 2) and B (5, 4) on graph paper. Take 2 cm = 1 unit on both the axes.
- Reflect A and B in the x-axis to A’ and B’ respectively. Plot these points also on the same graph paper.
- Write down:
- the geometrical name of the figure ABB’A’;
- the measure of angle ABB’;
- the image of A” of A, when A is reflected in the origin.
- the single transformation that maps A’ to A”.
Solution
- ∵ From the graph, we can say that
- ∵ Mx (x, y) = (x, –y)
Thus, Mx (3, 2) = (3, –2) and Mx (5, 4) = (5, –4) -
- an isosceles trapezium
- 45°
- ∵ Mo (x, y) = (–x, –y)
- Now A' (3, –2) `\implies` A" (–3, –2) ...[∵ My (x, y) = (–x, y)]
APPEARS IN
RELATED QUESTIONS
Points (3, 0) and (–1, 0) are invariant points under reflection in the line L1; points (0, –3) and (0, 1) are invariant points on reflection in line L2.
- Name or write equations for the lines L1 and L2.
- Write down the images of the points P (3, 4) and Q (–5, –2) on reflection in line L1. Name the images as P’ and Q’ respectively.
- Write down the images of P and Q on reflection in L2. Name the images as P” and Q” respectively.
- State or describe a single transformation that maps P’ onto P''.
- Point P (a, b) is reflected in the x-axis to P’ (5, –2). Write down the values of a and b.
- P” is the image of P when reflected in the y-axis. Write down the co-ordinates of P”.
- Name a single transformation that maps P’ to P”.
The point (–2, 0) on reflection in a line is mapped to (2, 0) and the point (5, –6) on reflection in the same line is mapped to (–5, –6).
- State the name of the mirror line and write its equation.
- State the co-ordinates of the image of (–8, –5) in the mirror line.
Points A and B have co-ordinates (3, 4) and (0, 2) respectively. Find the image:
- A’ of A under reflection in the x-axis.
- B’ of B under reflection in the line AA’.
- A” of A under reflection in the y-axis.
- B” of B under reflection in the line AA”.
The point P (5, 3) was reflected in the origin to get the image P’.
- Write down the co-ordinates of P’.
- If M is the foot of the perpendicular from P to the x-axis, find the co-ordinates of M.
- If N is the foot of the perpendicular from P’ to the x-axis, find the co-ordinates of N.
- Name the figure PMP’N.
- Find the area of the figure PMP’N.
A (1, 1), B (5, 1), C (4, 2) and D (2, 2) are vertices of a quadrilateral. Name the quadrilateral ABCD. A, B, C, and D are reflected in the origin on to A’, B’, C’ and D’ respectively. Locate A’, B’, C’ and D’ on the graph sheet and write their co-ordinates. Are D, A, A’ and D’ collinear?
A’ and B’ are images of A (-3, 5) and B (-5, 3) respectively on reflection in y-axis. Find: (
a) the co-ordinates of A’ and B’.
(b) Assign special name of quadrilateral AA’B’B.
(c) Are AB’ and BA’ equal in length?
Using a graph paper, plot the point A (6, 4) and B (0, 4).
(a) Reflect A and B in the origin to get the image A’ and B’.
(b) Write the co-ordinates of A’ and B’.
(c) Sate the geometrical name for the figure ABA’B’.
(d) Find its perimeter.
Use a graph paper for this question.
(Take 2 cm = 1 unit on both x and y axes)
- Plot the following points: A(0, 4), B(2, 3), C(1, 1) and D(2, 0).
- Reflect points B, C, D on the y-axis and write down their coordinates. Name the images as B', C', D' respectively.
- Join the points A, B, C, D, D', C', B' and A in order, so as to form a closed figure. Write down the equation to the line about which if this closed figure obtained is folded, the two parts of the figure exactly coincide.
Points (3, 0) and (-1, 0) are invarient points under reflection in the line L1; point (0, -3) and (0, 1) are invarient points on reflection in line L2.
(i) Write the equation of the line L1 and L2.
(ii) Write down the images of points P(3, 4) and Q(-5, -2) on reflection in L1. Name the images as P' and Q' respectively.
(iii) Write down the images of P and Q on reflection in L2. Name the image as P'' and Q'' respectively.
