Advertisements
Advertisements
Question
Box I contains two white and three black balls. Box II contains four white and one black balls and box III contains three white ·and four black balls. A dice having three red, two yellow and one green face, is thrown to select the box. If red face turns up, we pick up the box I, if a yellow face turns up we pick up box II, otherwise, we pick up box III. Then, we draw a ball from the selected box. If the ball is drawn is white, what is the probability that the dice had turned up with a red face?
Solution
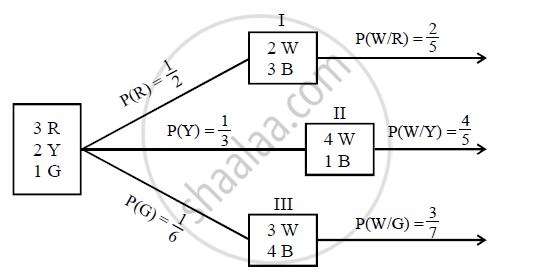
P(Total) = `1/2 xx 2/5 + 1/3 xx 4/5 + 1/6 xx 3/7`
`=1/5 + 4/15 + 1/14`
`= (42 + 56 + 15)/210`
`= 113/210`
`P(R"/"W) = (P(R).P(W"/"R))/"P(Total)"`
`= (1/2 xx 2/5)/(113/210)`
`= 1/5 xx 210/113`
`= 42/113`
APPEARS IN
RELATED QUESTIONS
Given that E and F are events such that P(E) = 0.6, P(F) = 0.3 and P(E ∩ F) = 0.2, find P (E|F) and P(F|E).
If `P(A) = 6/11, P(B) = 5/11 "and" P(A ∪ B) = 7/11` find
- P(A ∩ B)
- P(A|B)
- P(B|A)
Determine P(E|F).
A coin is tossed three times, where
E: head on third toss, F: heads on first two tosses
A black and a red dice are rolled.
Find the conditional probability of obtaining a sum greater than 9, given that the black die resulted in a 5.
A black and a red dice are rolled.
Find the conditional probability of obtaining the sum 8, given that the red die resulted in a number less than 4.
An instructor has a question bank consisting of 300 easy True/False questions, 200 difficult True/False questions, 500 easy multiple choice questions and 400 difficult multiple choice questions. If a question is selected at random from the question bank, what is the probability that it will be an easy question given that it is a multiple-choice question?
If a leap year is selected at random, what is the chance that it will contain 53 Tuesdays?
A card is drawn from a well-shuffled pack of playing cards. What is the probability that it is either a spade or an ace or both?
Bag A contains 4 white balls and 3 black balls. While Bag B contains 3 white balls and 5 black balls. Two balls are drawn from Bag A and placed in Bag B. Then, what is the probability of drawing a white ball from Bag B?
Two dice are thrown simultaneously, If at least one of the dice show a number 5, what is the probability that sum of the numbers on two dice is 9?
In an examination, 30% of students have failed in subject I, 20% of the students have failed in subject II and 10% have failed in both subject I and subject II. A student is selected at random, what is the probability that the student has failed in subject I, if it is known that he is failed in subject II?
A bag contains 10 white balls and 15 black balls. Two balls are drawn in succession without replacement. What is the probability that, first is white and second is black?
Three fair coins are tossed. What is the probability of getting three heads given that at least two coins show heads?
Select the correct option from the given alternatives :
Bag I contains 3 red and 4 black balls while another Bag II contains 5 red and 6 black balls. One ball is drawn at random from one of the bags and it is found to be red. The probability that it was drawn from Bag II
The probability that a car being filled with petrol will also need an oil change is 0.30; the probability that it needs a new oil filter is 0.40; and the probability that both the oil and filter need changing is 0.15. If the oil had to be changed, what is the probability that a new oil filter is needed?
One bag contains 5 white and 3 black balls. Another bag contains 4 white and 6 black balls. If one ball is drawn from each bag, find the probability that both are black
Choose the correct alternative:
A, B, and C try to hit a target simultaneously but independently. Their respective probabilities of hitting the target are `3/4, 1/2, 5/8`. The probability that the target is hit by A or B but not by C is
If X denotes the number of ones in five consecutive throws of a dice, then P(X = 4) is ______
Two dice are thrown. Find the probability that the sum of numbers appearing is more than 11, is ______.
The total number of ways in which 5 balls of different colours can be distributed among 3 persons so that each person gets at least one ball is ______
Three machines E1, E2, E3 in a certain factory produced 50%, 25% and 25%, respectively, of the total daily output of electric tubes. It is known that 4% of the tubes produced one each of machines E1 and E2 are defective, and that 5% of those produced on E3 are defective. If one tube is picked up at random from a day’s production, calculate the probability that it is defective.
Let A and B be two events. If P(A) = 0.2, P(B) = 0.4, P(A ∪ B) = 0.6, then P(A|B) is equal to ______.
If P(A) = `3/10`, P(B) = `2/5` and P(A ∪ B) = `3/5`, then P(B|A) + P(A|B) equals ______.
Two cards are drawn out randomly from a pack of 52 cards one after the other, without replacement. The probability of first card being a king and second card not being a king is:
If two balls are drawn from a bag containing 3 white, 4 black and 5 red balls. Then, the probability that the drawn balls are of different colours is:
A pack of cards has one card missing. Two cards are drawn randomly and are found to be spades. The probability that the missing card is not a spade, is ______.
Let A and B be two non-null events such that A ⊂ B. Then, which of the following statements is always correct?
If A and B are two events such that `P(A/B) = 2 xx P(B/A)` and P(A) + P(B) = `2/3`, then P(B) is equal to ______.
Three friends go to a restaurant to have pizza. They decide who will pay for the pizza by tossing a coin. It is decided that each one of them will toss a coin and if one person gets a different result (heads or tails) than the other two, that person would pay. If all three get the same result (all heads or all tails), they will toss again until they get a different result.
- What is the probability that all three friends will get the same result (all heads or all tails) in one round of tossing?
- What is the probability that they will get a different result in one round of tossing?
- What is the probability that they will need exactly four rounds of tossing to determine who would pay?
