Advertisements
Advertisements
प्रश्न
Box I contains two white and three black balls. Box II contains four white and one black balls and box III contains three white ·and four black balls. A dice having three red, two yellow and one green face, is thrown to select the box. If red face turns up, we pick up the box I, if a yellow face turns up we pick up box II, otherwise, we pick up box III. Then, we draw a ball from the selected box. If the ball is drawn is white, what is the probability that the dice had turned up with a red face?
उत्तर
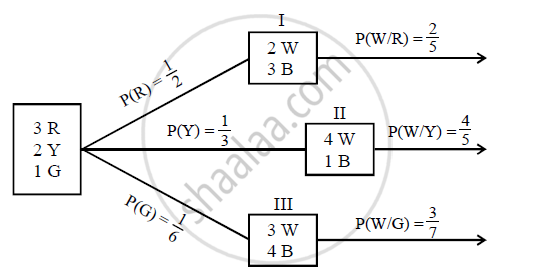
P(Total) = `1/2 xx 2/5 + 1/3 xx 4/5 + 1/6 xx 3/7`
`=1/5 + 4/15 + 1/14`
`= (42 + 56 + 15)/210`
`= 113/210`
`P(R"/"W) = (P(R).P(W"/"R))/"P(Total)"`
`= (1/2 xx 2/5)/(113/210)`
`= 1/5 xx 210/113`
`= 42/113`
APPEARS IN
संबंधित प्रश्न
Assume that each born child is equally likely to be a boy or a girl. If a family has two children, what is the conditional probability that both are girls? Given that
- the youngest is a girl.
- at least one is a girl.
An insurance agent insures lives of 5 men, all of the same age and in good health. The probability that a man of this age will survive the next 30 years is known to be 2/3 . Find the probability that in the next 30 years at most 3 men will survive.
If P(A) = 0.8, P(B) = 0.5 and P(B|A) = 0.4, find
- P(A ∩ B)
- P(A|B)
- P(A ∪ B)
Determine P(E|F).
A coin is tossed three times, where
E: head on third toss, F: heads on first two tosses
Determine P(E|F).
Two coins are tossed once, where
E: no tail appears, F: no head appears
Determine P(E|F).
A die is thrown three times,
E: 4 appears on the third toss, F: 6 and 5 appears respectively on first two tosses
A fair die is rolled. Consider events E = {1, 3, 5}, F = {2, 3} and G = {2, 3, 4, 5} Find P (E|F) and P (F|E)
Given that the two numbers appearing on throwing the two dice are different. Find the probability of the event ‘the sum of numbers on the dice is 4’.
In a game, a man wins a rupee for a six and loses a rupee for any other number when a fair die is thrown. The man decided to throw a die thrice but to quit as and when he gets a six. Find the expected value of the amount he wins/loses.
A die is thrown again and again until three sixes are obtained. Find the probability of obtaining the third six in the sixth throw of the die.
Five dice are thrown simultaneously. If the occurrence of an odd number in a single dice is considered a success, find the probability of maximum three successes.
Two balls are drawn from an urn containing 3 white, 5 red and 2 black balls, one by one without replacement. What is the probability that at least one ball is red?
Bag A contains 4 white balls and 3 black balls. While Bag B contains 3 white balls and 5 black balls. Two balls are drawn from Bag A and placed in Bag B. Then, what is the probability of drawing a white ball from Bag B?
In a college, 70% of students pass in Physics, 75% pass in Mathematics and 10% of students fail in both. One student is chosen at random. What is the probability that:
(i) He passes in Physics and Mathematics?
(ii) He passes in Mathematics given that he passes in Physics.
(iii) He passes in Physics given that he passes in Mathematics.
A bag contains 10 white balls and 15 black balls. Two balls are drawn in succession without replacement. What is the probability that, first is white and second is black?
A problem in Mathematics is given to three students whose chances of solving it are `1/3, 1/4` and `1/5`. What is the probability that the problem is solved?
A problem in Mathematics is given to three students whose chances of solving it are `1/3, 1/4` and `1/5`. What is the probability that exactly one of them will solve it?
One bag contains 5 white and 3 black balls. Another bag contains 4 white and 6 black balls. If one ball is drawn from each bag, find the probability that both are white
One bag contains 5 white and 3 black balls. Another bag contains 4 white and 6 black balls. If one ball is drawn from each bag, find the probability that one white and one black
Choose the correct alternative:
If two events A and B are independent such that P(A) = 0.35 and P(A ∪ B) = 0.6, then P(B) is
In a multiple-choice question, there are three options out of which only one is correct. A person is guessing the answer at random. If there are 7 such questions, then the probability that he will get exactly 4 correct answers is ______
Two dice are thrown. Find the probability that the sum of numbers appearing is more than 11, is ______.
If P(A) = `2/5`, P(B) = `3/10` and P(A ∩ B) = `1/5`, then P(A|B).P(B'|A') is equal to ______.
Two cards are drawn out randomly from a pack of 52 cards one after the other, without replacement. The probability of first card being a king and second card not being a king is:
A bag contains 6 red and 5 blue balls and another bag contains 5 red and 8 blue balls. A ball is drawn from the first bag and without noticing its colour is placed in the second bag. If a ball is drawn from the second bag, then find the probability that the drawn ball is red in colour.
A bag contains 3 red and 4 white balls and another bag contains 2 red and 3 white balls. If one ball is drawn from the first bag and 2 balls are drawn from the second bag, then find the probability that all three balls are of the same colour.
If A and B are two events such that P(A) = `1/3`, P(B) = `1/5` and P(A ∪ B) = `1/2`, then P(A|B') + P(B|A') is equal to ______.
For a biased dice, the probability for the different faces to turn up are
| Face | 1 | 2 | 3 | 4 | 5 | 6 |
| P | 0.10 | 0.32 | 0.21 | 0.15 | 0.05 | 0.17 |
The dice is tossed and it is told that either the face 1 or face 2 has shown up, then the probability that it is face 1, is ______.
Students of under graduation submitted a case study on “Understanding the Probability of Left-Handedness in Children Based on Parental Handedness”. Following Recent studies suggest that roughly 12% of the world population is left-handed. Depending on the parents’ handedness, the chances of having a left-handed child are as follows:
Scenario A: Both parents are left-handed, with a 24% chance of the child being left-handed.
Scenario B: The fathers is right-handed and the mothers left-handed, with a 22% chance of child being left-handed.
Scenario C: The fathers left-handed and the mother is right-handed, with a 17% chance of child being left-handed.
Scenario D: Both parents are right-handed, with a 9% chance of having a left-handed child.
Assuming that scenarios A, B, C and D are equally likely and L denotes the event that the child is left-handed, answer the following questions.
- What is the overall probability that a randomly selected child is left-handed?
- Given that exactly one parent is left-handed, what is the probability that a randomly selected child is left-handed?
- If a child is left-handed, what is the probability that both parents are left-handed?
