Advertisements
Advertisements
प्रश्न
A die is thrown again and again until three sixes are obtained. Find the probability of obtaining the third six in the sixth throw of the die.
उत्तर
The probability of getting a six in a throw of die 1/6 and not getting a six is 5/6.
Let `p = 1/6 and q = 5/6`
The probability that the 2 sixes come in the first five throws of the die is `""^5C_2 (1/6)^2(5/6)^3 = (10xx(5)^3)/(6)^5 `
∴ Probability that third six comes in the sixth throw `(10xx(5)^3)/(6)^5 xx 1/6`
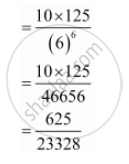
APPEARS IN
संबंधित प्रश्न
Assume that each born child is equally likely to be a boy or a girl. If a family has two children, what is the conditional probability that both are girls? Given that
- the youngest is a girl.
- at least one is a girl.
An insurance agent insures lives of 5 men, all of the same age and in good health. The probability that a man of this age will survive the next 30 years is known to be 2/3 . Find the probability that in the next 30 years at most 3 men will survive.
If P(A) = 0.8, P(B) = 0.5 and P(B|A) = 0.4, find
- P(A ∩ B)
- P(A|B)
- P(A ∪ B)
Determine P(E|F).
A coin is tossed three times, where
E: head on third toss, F: heads on first two tosses
Determine P(E|F).
Two coins are tossed once, where
E: tail appears on one coin, F: one coin shows head
A fair die is rolled. Consider events E = {1, 3, 5}, F = {2, 3} and G = {2, 3, 4, 5} Find P (E|F) and P (F|E)
An instructor has a question bank consisting of 300 easy True/False questions, 200 difficult True/False questions, 500 easy multiple choice questions and 400 difficult multiple choice questions. If a question is selected at random from the question bank, what is the probability that it will be an easy question given that it is a multiple-choice question?
Two balls are drawn at random with replacement from a box containing 10 black and 8 red balls. Find the probability that
- both balls are red.
- first ball is black and second is red.
- one of them is black and other is red.
If A and B are events such as that P(A) = `1/2`, P(B) = `1/3` and P(A ∩ B) = `1/4`, then find
1) P(A / B)
2) P(B / A)
A card is drawn from a well-shuffled pack of playing cards. What is the probability that it is either a spade or an ace or both?
Five dice are thrown simultaneously. If the occurrence of an odd number in a single dice is considered a success, find the probability of maximum three successes.
A pair of dice is thrown. If sum of the numbers is an even number, what is the probability that it is a perfect square?
In an examination, 30% of students have failed in subject I, 20% of the students have failed in subject II and 10% have failed in both subject I and subject II. A student is selected at random, what is the probability that the student has failed in at least one subject?
An urn contains 4 black, 5 white, and 6 red balls. Two balls are drawn one after the other without replacement, What is the probability that at least one ball is black?
From a pack of well-shuffled cards, two cards are drawn at random. Find the probability that both the cards are diamonds when first card drawn is kept aside
From a pack of well-shuffled cards, two cards are drawn at random. Find the probability that both the cards are diamonds when the first card drawn is replaced in the pack
Two cards are drawn one after the other from a pack of 52 cards without replacement. What is the probability that both the cards drawn are face cards?
Select the correct option from the given alternatives :
Bag I contains 3 red and 4 black balls while another Bag II contains 5 red and 6 black balls. One ball is drawn at random from one of the bags and it is found to be red. The probability that it was drawn from Bag II
Can two events be mutually exclusive and independent simultaneously?
If A and B are two independent events such that P(A ∪ B) = 0.6, P(A) = 0.2, find P(B)
A problem in Mathematics is given to three students whose chances of solving it are `1/3, 1/4` and `1/5`. What is the probability that the problem is solved?
A problem in Mathematics is given to three students whose chances of solving it are `1/3, 1/4` and `1/5`. What is the probability that exactly one of them will solve it?
Two thirds of students in a class are boys and rest girls. It is known that the probability of a girl getting a first grade is 0.85 and that of boys is 0.70. Find the probability that a student chosen at random will get first grade marks.
Given P(A) = 0.4 and P(A ∪ B) = 0.7 Find P(B) if P(A/B) = 0.4
Choose the correct alternative:
A, B, and C try to hit a target simultaneously but independently. Their respective probabilities of hitting the target are `3/4, 1/2, 5/8`. The probability that the target is hit by A or B but not by C is
Choose the correct alternative:
If A and B are any two events, then the probability that exactly one of them occur is
Two dice are thrown. Find the probability that the sum of numbers appearing is more than 11, is ______.
Three machines E1, E2, E3 in a certain factory produced 50%, 25% and 25%, respectively, of the total daily output of electric tubes. It is known that 4% of the tubes produced one each of machines E1 and E2 are defective, and that 5% of those produced on E3 are defective. If one tube is picked up at random from a day’s production, calculate the probability that it is defective.
If P(A ∩ B) = `7/10` and P(B) = `17/20`, then P(A|B) equals ______.
If P(A) = `3/10`, P(B) = `2/5` and P(A ∪ B) = `3/5`, then P(B|A) + P(A|B) equals ______.
If P(A) = `2/5`, P(B) = `3/10` and P(A ∩ B) = `1/5`, then P(A|B).P(B'|A') is equal to ______.
A bag contains 3 red and 4 white balls and another bag contains 2 red and 3 white balls. If one ball is drawn from the first bag and 2 balls are drawn from the second bag, then find the probability that all three balls are of the same colour.
If P(A) = `1/2`, P(B) = 0, then `P(A/B)` is
Compute P(A|B), if P(B) = 0.5 and P (A ∩ B) = 0.32.
