Advertisements
Advertisements
प्रश्न
A die is thrown again and again until three sixes are obtained. Find the probability of obtaining the third six in the sixth throw of the die.
उत्तर
The probability of getting a six in a throw of die 1/6 and not getting a six is 5/6.
Let `p = 1/6 and q = 5/6`
The probability that the 2 sixes come in the first five throws of the die is `""^5C_2 (1/6)^2(5/6)^3 = (10xx(5)^3)/(6)^5 `
∴ Probability that third six comes in the sixth throw `(10xx(5)^3)/(6)^5 xx 1/6`
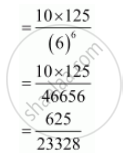
APPEARS IN
संबंधित प्रश्न
Assume that each born child is equally likely to be a boy or a girl. If a family has two children, what is the conditional probability that both are girls? Given that
- the youngest is a girl.
- at least one is a girl.
Assume that the chances of a patient having a heart attack is 40%. Assuming that a meditation and yoga course reduces the risk of heart attack by 30% and prescription of certain drug reduces its chance by 25%. At a time a patient can choose any one of the two options with equal probabilities. It is given that after going through one of the two options, the patient selected at random suffers a heart attack. Find the probability that the patient followed a course of meditation and yoga. Interpret the result and state which of the above stated methods is more beneficial for the patient.
The probability that a certain kind of component will survive a check test is 0.6. Find the probability that exactly 2 of the next 4 tested components survive
Determine P(E|F).
A coin is tossed three times, where
E: at most two tails, F: at least one tail
Determine P(E|F).
Two coins are tossed once, where
E: no tail appears, F: no head appears
A fair die is rolled. Consider events E = {1, 3, 5}, F = {2, 3} and G = {2, 3, 4, 5} Find P (E|G) and P (G|E)
An instructor has a question bank consisting of 300 easy True/False questions, 200 difficult True/False questions, 500 easy multiple choice questions and 400 difficult multiple choice questions. If a question is selected at random from the question bank, what is the probability that it will be an easy question given that it is a multiple-choice question?
If P(A) = `1/2`, P(B) = 0, then P(A|B) is ______.
In a game, a man wins a rupee for a six and loses a rupee for any other number when a fair die is thrown. The man decided to throw a die thrice but to quit as and when he gets a six. Find the expected value of the amount he wins/loses.
Suppose we have four boxes. A, B, C and D containing coloured marbles as given below:
| Box | Marble colour | ||
| Red | White | Black | |
| A | 1 | 6 | 3 |
| B | 6 | 2 | 2 |
| C | 8 | 1 | 1 |
| D | 0 | 6 | 4 |
One of the boxes has been selected at random and a single marble is drawn from it. If the marble is red, what is the probability that it was drawn from box A?, box B?, box C?
A card is drawn from a well-shuffled pack of playing cards. What is the probability that it is either a spade or an ace or both?
An urn contains 2 white and 2 black balls. A ball is drawn at random. If it is white, it is not replaced into the urn. Otherwise, it is replaced with another ball of the same colour. The process is repeated. Find the probability that the third ball is drawn is black.
Three cards are drawn at random (without replacement) from a well-shuffled pack of 52 playing cards. Find the probability distribution of the number of red cards. Hence, find the mean of the distribution.
Two balls are drawn from an urn containing 3 white, 5 red and 2 black balls, one by one without replacement. What is the probability that at least one ball is red?
If events A and B are independent, such that `P(A)= 3/5`, `P(B)=2/3` 'find P(A ∪ B).
Two dice are thrown simultaneously, If at least one of the dice show a number 5, what is the probability that sum of the numbers on two dice is 9?
In an examination, 30% of students have failed in subject I, 20% of the students have failed in subject II and 10% have failed in both subject I and subject II. A student is selected at random, what is the probability that the student has failed in subject I, if it is known that he is failed in subject II?
A bag contains 10 white balls and 15 black balls. Two balls are drawn in succession without replacement. What is the probability that, first is white and second is black?
Two balls are drawn from an urn containing 5 green, 3 blue, and 7 yellow balls one by one without replacement. What is the probability that at least one ball is blue?
Two cards are drawn one after the other from a pack of 52 cards without replacement. What is the probability that both the cards drawn are face cards?
Can two events be mutually exclusive and independent simultaneously?
A problem in Mathematics is given to three students whose chances of solving it are `1/3, 1/4` and `1/5`. What is the probability that the problem is solved?
A problem in Mathematics is given to three students whose chances of solving it are `1/3, 1/4` and `1/5`. What is the probability that exactly one of them will solve it?
The probability that a car being filled with petrol will also need an oil change is 0.30; the probability that it needs a new oil filter is 0.40; and the probability that both the oil and filter need changing is 0.15. If the oil had to be changed, what is the probability that a new oil filter is needed?
The probability that a car being filled with petrol will also need an oil change is 0.30; the probability that it needs a new oil filter is 0.40; and the probability that both the oil and filter need changing is 0.15. If a new oil filter is needed, what is the probability that the oil has to be changed?
One bag contains 5 white and 3 black balls. Another bag contains 4 white and 6 black balls. If one ball is drawn from each bag, find the probability that one white and one black
Two thirds of students in a class are boys and rest girls. It is known that the probability of a girl getting a first grade is 0.85 and that of boys is 0.70. Find the probability that a student chosen at random will get first grade marks.
A year is selected at random. What is the probability that it is a leap year which contains 53 Sundays
Choose the correct alternative:
A letter is taken at random from the letters of the word ‘ASSISTANT’ and another letter is taken at random from the letters of the word ‘STATISTICS’. The probability that the selected letters are the same is
Two dice are thrown. Find the probability that the sum of numbers appearing is more than 11, is ______.
The total number of ways in which 5 balls of different colours can be distributed among 3 persons so that each person gets at least one ball is ______
Three machines E1, E2, E3 in a certain factory produced 50%, 25% and 25%, respectively, of the total daily output of electric tubes. It is known that 4% of the tubes produced one each of machines E1 and E2 are defective, and that 5% of those produced on E3 are defective. If one tube is picked up at random from a day’s production, calculate the probability that it is defective.
If the sum of numbers obtained on throwing a pair of dice is 9, then the probability that number obtained on one of the dice is 4, is ______.
If A and B are two events such that `P(A/B) = 2 xx P(B/A)` and P(A) + P(B) = `2/3`, then P(B) is equal to ______.
Three friends go to a restaurant to have pizza. They decide who will pay for the pizza by tossing a coin. It is decided that each one of them will toss a coin and if one person gets a different result (heads or tails) than the other two, that person would pay. If all three get the same result (all heads or all tails), they will toss again until they get a different result.
- What is the probability that all three friends will get the same result (all heads or all tails) in one round of tossing?
- What is the probability that they will get a different result in one round of tossing?
- What is the probability that they will need exactly four rounds of tossing to determine who would pay?
Students of under graduation submitted a case study on “Understanding the Probability of Left-Handedness in Children Based on Parental Handedness”. Following Recent studies suggest that roughly 12% of the world population is left-handed. Depending on the parents’ handedness, the chances of having a left-handed child are as follows:
Scenario A: Both parents are left-handed, with a 24% chance of the child being left-handed.
Scenario B: The fathers is right-handed and the mothers left-handed, with a 22% chance of child being left-handed.
Scenario C: The fathers left-handed and the mother is right-handed, with a 17% chance of child being left-handed.
Scenario D: Both parents are right-handed, with a 9% chance of having a left-handed child.
Assuming that scenarios A, B, C and D are equally likely and L denotes the event that the child is left-handed, answer the following questions.
- What is the overall probability that a randomly selected child is left-handed?
- Given that exactly one parent is left-handed, what is the probability that a randomly selected child is left-handed?
- If a child is left-handed, what is the probability that both parents are left-handed?
