Advertisements
Advertisements
Question
A die is thrown again and again until three sixes are obtained. Find the probability of obtaining the third six in the sixth throw of the die.
Solution
The probability of getting a six in a throw of die 1/6 and not getting a six is 5/6.
Let `p = 1/6 and q = 5/6`
The probability that the 2 sixes come in the first five throws of the die is `""^5C_2 (1/6)^2(5/6)^3 = (10xx(5)^3)/(6)^5 `
∴ Probability that third six comes in the sixth throw `(10xx(5)^3)/(6)^5 xx 1/6`
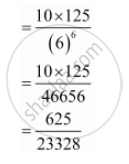
APPEARS IN
RELATED QUESTIONS
40% students of a college reside in hostel and the remaining reside outside. At the end of the year, 50% of the hostelers got A grade while from outside students, only 30% got A grade in the examination. At the end of the year, a student of the college was chosen at random and was found to have gotten A grade. What is the probability that the selected student was a hosteler ?
If P(A) = 0.8, P(B) = 0.5 and P(B|A) = 0.4, find
- P(A ∩ B)
- P(A|B)
- P(A ∪ B)
Evaluate P(A ∪ B), if 2P(A) = P(B) = `5/13` and P(A | B) = `2/5`
Determine P(E|F).
A coin is tossed three times, where
E: head on third toss, F: heads on first two tosses
Determine P(E|F).
Two coins are tossed once, where
E: no tail appears, F: no head appears
A die is tossed thrice. Find the probability of getting an odd number at least once.
A and B are two events such that P (A) ≠ 0. Find P (B|A), if A is a subset of B.
A and B are two events such that P (A) ≠ 0. Find P (B|A), if A ∩ B = Φ.
In a game, a man wins a rupee for a six and loses a rupee for any other number when a fair die is thrown. The man decided to throw a die thrice but to quit as and when he gets a six. Find the expected value of the amount he wins/loses.
An urn contains 2 white and 2 black balls. A ball is drawn at random. If it is white, it is not replaced into the urn. Otherwise, it is replaced with another ball of the same colour. The process is repeated. Find the probability that the third ball is drawn is black.
Five dice are thrown simultaneously. If the occurrence of an odd number in a single dice is considered a success, find the probability of maximum three successes.
A box has 20 pens of which 2 are defective. Calculate the probability that out of 5 pens drawn one by one with replacement, at most 2 are defective.
Three cards are drawn at random (without replacement) from a well-shuffled pack of 52 playing cards. Find the probability distribution of the number of red cards. Hence, find the mean of the distribution.
Bag A contains 4 white balls and 3 black balls. While Bag B contains 3 white balls and 5 black balls. Two balls are drawn from Bag A and placed in Bag B. Then, what is the probability of drawing a white ball from Bag B?
In a college, 70% of students pass in Physics, 75% pass in Mathematics and 10% of students fail in both. One student is chosen at random. What is the probability that:
(i) He passes in Physics and Mathematics?
(ii) He passes in Mathematics given that he passes in Physics.
(iii) He passes in Physics given that he passes in Mathematics.
In an examination, 30% of students have failed in subject I, 20% of the students have failed in subject II and 10% have failed in both subject I and subject II. A student is selected at random, what is the probability that the student has failed in at least one subject?
A bag contains 10 white balls and 15 black balls. Two balls are drawn in succession without replacement. What is the probability that, first is white and second is black?
Two balls are drawn from an urn containing 5 green, 3 blue, and 7 yellow balls one by one without replacement. What is the probability that at least one ball is blue?
Two cards are drawn one after the other from a pack of 52 cards without replacement. What is the probability that both the cards drawn are face cards?
One bag contains 5 white and 3 black balls. Another bag contains 4 white and 6 black balls. If one ball is drawn from each bag, find the probability that both are white
Given P(A) = 0.4 and P(A ∪ B) = 0.7 Find P(B) if A and B are independent events
A year is selected at random. What is the probability that it is a leap year which contains 53 Sundays
Choose the correct alternative:
If A and B are any two events, then the probability that exactly one of them occur is
Choose the correct alternative:
If two events A and B are independent such that P(A) = 0.35 and P(A ∪ B) = 0.6, then P(B) is
A die is thrown nine times. If getting an odd number is considered as a success, then the probability of three successes is ______
Three machines E1, E2, E3 in a certain factory produced 50%, 25% and 25%, respectively, of the total daily output of electric tubes. It is known that 4% of the tubes produced one each of machines E1 and E2 are defective, and that 5% of those produced on E3 are defective. If one tube is picked up at random from a day’s production, calculate the probability that it is defective.
If P(A) = `3/10`, P(B) = `2/5` and P(A ∪ B) = `3/5`, then P(B|A) + P(A|B) equals ______.
If two balls are drawn from a bag containing 3 white, 4 black and 5 red balls. Then, the probability that the drawn balls are of different colours is:
A bag contains 3 red and 4 white balls and another bag contains 2 red and 3 white balls. If one ball is drawn from the first bag and 2 balls are drawn from the second bag, then find the probability that all three balls are of the same colour.
If P(A) = `1/2`, P(B) = 0, then `P(A/B)` is
Let A and B be two non-null events such that A ⊂ B. Then, which of the following statements is always correct?
If A and B are two events such that P(A) = `1/3`, P(B) = `1/5` and P(A ∪ B) = `1/2`, then P(A|B') + P(B|A') is equal to ______.
For a biased dice, the probability for the different faces to turn up are
| Face | 1 | 2 | 3 | 4 | 5 | 6 |
| P | 0.10 | 0.32 | 0.21 | 0.15 | 0.05 | 0.17 |
The dice is tossed and it is told that either the face 1 or face 2 has shown up, then the probability that it is face 1, is ______.
It is given that the events A and B are such that P(A) = `1/4, P(A/B) = 1/2` and `P(B/A) = 2/3`, then P(B) is equal to ______.
If A and B are two independent events such that P(A) = `1/3` and P(B) = `1/4`, then `P(B^'/A)` is ______.
Three friends go to a restaurant to have pizza. They decide who will pay for the pizza by tossing a coin. It is decided that each one of them will toss a coin and if one person gets a different result (heads or tails) than the other two, that person would pay. If all three get the same result (all heads or all tails), they will toss again until they get a different result.
- What is the probability that all three friends will get the same result (all heads or all tails) in one round of tossing?
- What is the probability that they will get a different result in one round of tossing?
- What is the probability that they will need exactly four rounds of tossing to determine who would pay?
Compute P(A|B), if P(B) = 0.5 and P (A ∩ B) = 0.32.
