Advertisements
Advertisements
Question
In a hurdle race, a player has to cross 10 hurdles. The probability that he will clear each hurdle is 5/6 . What is the probability that he will knock down fewer than 2 hurdles?
Solution
Let p and q respectively be the probabilities that the player will clear and knock down the hurdle.
`:. p = 5/6`
`q = 1 - p = 1 - 5/6 = 1/6`
Let X be the random variable that represents the number of times the player will knock down the hurdle.
Therefore, by binomial distribution, we obtain
P (X = x) = `""^nC_x p^(n-x) q^x`
P (player knocking down less than 2 hurdles) = P (X < 2)
= P (X = 0) + P (X = 1)
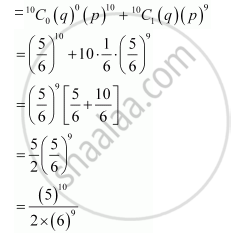
APPEARS IN
RELATED QUESTIONS
A bag consists of 10 balls each marked with one of the digits 0 to 9. If four balls are drawn successively with replacement from the bag, what is the probability that none is marked with the digit 0?
A person buys a lottery ticket in 50 lotteries, in each of which his chance of winning a prize is 1/100. What is the probability that he will in a prize (a) at least once (b) exactly once (c) at least twice?
The probability that a student is not a swimmer is 1/5 . Then the probability that out of five students, four are swimmers is
(A) `""^5C_4 (4/5)^4 1/5`
(B) `(4/5)^4 1/5
(C) `""^5C_1 1/5 (4/5)^4 `
(D) None of these
A fair coin is tossed 9 times. Find the probability that it shows head exactly 5 times.
Five cards are drawn successively with replacement from a well-shuffled pack of 52 cards. What is the probability that all the five cards are spades ?
A bag contains 10 balls, each marked with one of the digits from 0 to 9. If four balls are drawn successively with replacement from the bag, what is the probability that none is marked with the digit 0?
An urn contains four white and three red balls. Find the probability distribution of the number of red balls in three draws with replacement from the urn.
A card is drawn and replaced in an ordinary pack of 52 cards. How many times must a card be drawn so that (i) there is at least an even chance of drawing a heart (ii) the probability of drawing a heart is greater than 3/4?
Assume that the probability that a bomb dropped from an aeroplane will strike a certain target is 0.2. If 6 bombs are dropped, find the probability that at least 2 will strike the target
It is known that 60% of mice inoculated with a serum are protected from a certain disease. If 5 mice are inoculated, find the probability that more than 3 contract the disease .
In a hospital, there are 20 kidney dialysis machines and the chance of any one of them to be out of service during a day is 0.02. Determine the probability that exactly 3 machines will be out of service on the same day.
A person buys a lottery ticket in 50 lotteries, in each of which his chance of winning a prize is `1/100`. What is the probability that he will win a prize at least once.
A person buys a lottery ticket in 50 lotteries, in each of which his chance of winning a prize is \[\frac{1}{100} .\] What is the probability that he will win a prize at least twice.
The probability of a shooter hitting a target is \[\frac{3}{4} .\] How many minimum number of times must he/she fire so that the probability of hitting the target at least once is more than 0.99?
A die is thrown 5 times. Find the probability that an odd number will come up exactly three times.
A factory produces bulbs. The probability that one bulb is defective is \[\frac{1}{50}\] and they are packed in boxes of 10. From a single box, find the probability that exactly two bulbs are defective
A factory produces bulbs. The probability that one bulb is defective is \[\frac{1}{50}\] and they are packed in boxes of 10. From a single box, find the probability that more than 8 bulbs work properly
If the probability of a defective bolt is 0.1, find the (i) mean and (ii) standard deviation for the distribution of bolts in a total of 400 bolts.
The mean and variance of a binomial variate with parameters n and p are 16 and 8, respectively. Find P (X = 0), P (X = 1) and P (X ≥ 2).
If X follows a binomial distribution with mean 4 and variance 2, find P (X ≥ 5).
A die is tossed twice. A 'success' is getting an even number on a toss. Find the variance of number of successes.
If in a binomial distribution mean is 5 and variance is 4, write the number of trials.
An unbiased coin is tossed 4 times. Find the mean and variance of the number of heads obtained.
If in a binomial distribution n = 4, P (X = 0) = \[\frac{16}{81}\], then P (X = 4) equals
A rifleman is firing at a distant target and has only 10% chance of hitting it. The least number of rounds he must fire in order to have more than 50% chance of hitting it at least once is
A fair coin is tossed 100 times. The probability of getting tails an odd number of times is
A biased coin with probability p, 0 < p < 1, of heads is tossed until a head appears for the first time. If the probability that the number of tosses required is even is 2/5, then p equals
A five-digit number is written down at random. The probability that the number is divisible by 5, and no two consecutive digits are identical, is
A coin is tossed 10 times. The probability of getting exactly six heads is
A coin is tossed 4 times. The probability that at least one head turns up is
Mark the correct alternative in the following question:
Suppose a random variable X follows the binomial distribution with parameters n and p, where 0 < p < 1. If \[\frac{P\left( X = r \right)}{P\left( X = n - r \right)}\] is independent of n and r, then p equals
Five cards are drawn successively with replacement from a well-shuffled pack of 52 cards. What is the probability that none is a spade ?
Find the mean and variance of the random variable X which denotes the number of doublets in four throws of a pair of dice.
Explain why the experiment of tossing a coin three times is said to have binomial distribution.
If x4 occurs in the tth term in the expansion of `(x^4 + 1/x^3)^15`, then the value oft is equal to:
If a random variable X follows the Binomial distribution B(5, p) such that P(X = 0) = P(X = 1), then `(P(X = 2))/(P(X = 3))` is equal to ______.
