Advertisements
Advertisements
प्रश्न
In a hurdle race, a player has to cross 10 hurdles. The probability that he will clear each hurdle is 5/6 . What is the probability that he will knock down fewer than 2 hurdles?
उत्तर
Let p and q respectively be the probabilities that the player will clear and knock down the hurdle.
`:. p = 5/6`
`q = 1 - p = 1 - 5/6 = 1/6`
Let X be the random variable that represents the number of times the player will knock down the hurdle.
Therefore, by binomial distribution, we obtain
P (X = x) = `""^nC_x p^(n-x) q^x`
P (player knocking down less than 2 hurdles) = P (X < 2)
= P (X = 0) + P (X = 1)
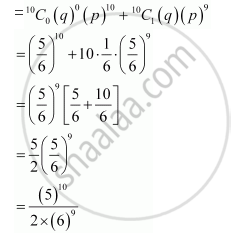
APPEARS IN
संबंधित प्रश्न
A fair coin is tossed 8 times. Find the probability that it shows heads at least once
A pair of dice is thrown 4 times. If getting a doublet is considered a success, find the probability of two successes.
A bag consists of 10 balls each marked with one of the digits 0 to 9. If four balls are drawn successively with replacement from the bag, what is the probability that none is marked with the digit 0?
A fair coin is tossed 9 times. Find the probability that it shows head exactly 5 times.
The probability of a man hitting a target is 1/4. If he fires 7 times, what is the probability of his hitting the target at least twice?
Eight coins are thrown simultaneously. Find the chance of obtaining at least six heads.
A bag contains 7 red, 5 white and 8 black balls. If four balls are drawn one by one with replacement, what is the probability that none is white ?
A bag contains 2 white, 3 red and 4 blue balls. Two balls are drawn at random from the bag. If X denotes the number of white balls among the two balls drawn, describe the probability distribution of X.
An urn contains four white and three red balls. Find the probability distribution of the number of red balls in three draws with replacement from the urn.
Find the probability distribution of the number of sixes in three tosses of a die.
Five dice are thrown simultaneously. If the occurrence of 3, 4 or 5 in a single die is considered a success, find the probability of at least 3 successes.
The items produced by a company contain 10% defective items. Show that the probability of getting 2 defective items in a sample of 8 items is
\[\frac{28 \times 9^6}{{10}^8} .\]
A card is drawn and replaced in an ordinary pack of 52 cards. How many times must a card be drawn so that (i) there is at least an even chance of drawing a heart (ii) the probability of drawing a heart is greater than 3/4?
The probability that a certain kind of component will survive a given shock test is \[\frac{3}{4} .\] Find the probability that among 5 components tested at most 3 will survive .
Assume that the probability that a bomb dropped from an aeroplane will strike a certain target is 0.2. If 6 bombs are dropped, find the probability that exactly 2 will strike the target .
The probability that a student entering a university will graduate is 0.4. Find the probability that out of 3 students of the university only one will graduate .
A person buys a lottery ticket in 50 lotteries, in each of which his chance of winning a prize is `1/100`. What is the probability that he will win a prize at least once.
A factory produces bulbs. The probability that one bulb is defective is \[\frac{1}{50}\] and they are packed in boxes of 10. From a single box, find the probability that none of the bulbs is defective .
If the mean and variance of a binomial distribution are respectively 9 and 6, find the distribution.
If on an average 9 ships out of 10 arrive safely at ports, find the mean and S.D. of the ships returning safely out of a total of 500 ships.
The mean and variance of a binomial variate with parameters n and p are 16 and 8, respectively. Find P (X = 0), P (X = 1) and P (X ≥ 2).
The mean and variance of a binomial distribution are \[\frac{4}{3}\] and \[\frac{8}{9}\] respectively. Find P (X ≥ 1).
A die is tossed twice. A 'success' is getting an even number on a toss. Find the variance of number of successes.
A die is thrown three times. Let X be 'the number of twos seen'. Find the expectation of X.
If the mean and variance of a random variable X with a binomial distribution are 4 and 2 respectively, find P (X = 1).
A fair coin is tossed 100 times. The probability of getting tails an odd number of times is
A fair coin is tossed 99 times. If X is the number of times head appears, then P (X = r) is maximum when r is
Fifteen coupons are numbered 1 to 15. Seven coupons are selected at random one at a time with replacement. The probability that the largest number appearing on a selected coupon is 9 is
Mark the correct alternative in the following question:
Suppose a random variable X follows the binomial distribution with parameters n and p, where 0 < p < 1. If \[\frac{P\left( X = r \right)}{P\left( X = n - r \right)}\] is independent of n and r, then p equals
Mark the correct alternative in the following question:
The probability that a person is not a swimmer is 0.3. The probability that out of 5 persons 4 are swimmers is
A bag contains 7 red, 5 white and 8 black balls. If four balls are drawn one by one with replacement, what is the probability that any two are white ?
The probability that a bulb produced by a factory will fuse after 150 days of use is 0.05. Find the probability that out of 5 such bulbs at least one will fuse after 150 days of use
Find the mean and variance of the random variable X which denotes the number of doublets in four throws of a pair of dice.
Bernoulli distribution is a particular case of binomial distribution if n = ______
Which one is not a requirement of a binomial distribution?
If X follows binomial distribution with parameters n = 5, p and P(X = 2) = 9, P(X = 3), then p = ______.
If X ∼ B(n, p), n = 6 and 9 P(X = 4) = P(X = 2), then find the value of p.
For the binomial distribution X ∼ B(n, p), n = 6 and P(X = 4) = P(X = 2). find p.
