Advertisements
Advertisements
Question
An urn contains 25 balls of which 10 balls bear a mark ‘X’ and the remaining 15 bear a mark ‘Y’. A ball is drawn at random from the urn, its mark is noted down and it is replaced. If 6 balls are drawn in this way, find the probability that
(i) all will bear ‘X’ mark.
(ii) not more than 2 will bear ‘Y’ mark.
(iii) at least one ball will bear ‘Y’ mark
(iv) the number of balls with ‘X’ mark and ‘Y’ mark will be equal.
Solution
Total number of balls in the urn = 25
Balls bearing mark ‘X’ = 10
Balls bearing mark ‘Y’ = 15
p = P (ball bearing mark ‘X’) =`10/25 = 2/5`
q = P (ball bearing mark ‘Y’) =`15/25 = 3/5`
Six balls are drawn with replacement. Therefore, the number of trials are Bernoulli trials.
Let Z be the random variable that represents the number of balls with ‘Y’ mark on them in the trials.
Clearly, Z has a binomial distribution with n = 6 and p = 2/5
∴ P (Z = z) = `""^nC_zp^(n-z)q^z`
(i) P (all will bear ‘X’ mark) = P (Z = 0) =`""^6C_0 (2/5)^6 = (2/5)^6`
(ii) P (not more than 2 bear ‘Y’ mark) = P (Z ≤ 2)
= P (Z = 0) + P (Z = 1) + P (Z = 2)
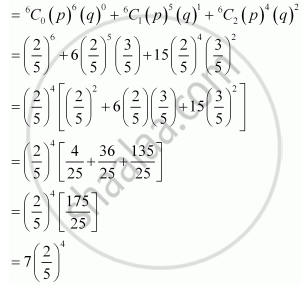
(iii) P (at least one ball bears ‘Y’ mark) = P (Z ≥ 1) = 1 − P (Z = 0)
`= 1 - (2/5)^6`
(iv) P (equal number of balls with ‘X’ mark and ‘Y’ mark) = P (Z = 3)
= C36 253 353
`= 20x8x27/15628`
`= 864/3125`
APPEARS IN
RELATED QUESTIONS
From a lot of 25 bulbs of which 5 are defective a sample of 5 bulbs was drawn at random with replacement. Find the probability that the sample will contain -
(a) exactly 1 defective bulb.
(b) at least 1 defective bulb.
From a lot of 30 bulbs which include 6 defectives, a sample of 4 bulbs is drawn at random with replacement. Find the probability distribution of the number of defective bulbs.
A random variable X has the following probability distribution.
| X | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| P(X) | 0 | k | 2k | 2k | 3k | k2 |
2k2 |
7k2 + k |
Determine
(i) k
(ii) P (X < 3)
(iii) P (X > 6)
(iv) P (0 < X < 3)
The random variable X has probability distribution P(X) of the following form, where k is some number:
`P(X = x) {(k, if x = 0),(2k, if x = 1),(3k, if x = 2),(0, "otherwise"):}`
- Determine the value of 'k'.
- Find P(X < 2), P(X ≥ 2), P(X ≤ 2).
If the probability that a fluorescent light has a useful life of at least 800 hours is 0.9, find the probabilities that among 20 such lights at least 2 will not have a useful life of at least 800 hours. [Given : (0⋅9)19 = 0⋅1348]
Three persons A, B and C shoot to hit a target. If A hits the target four times in five trials, B hits it three times in four trials and C hits it two times in three trials, find the probability that:
1) Exactly two persons hit the target.
2) At least two persons hit the target.
3) None hit the target.
Four cards are drawn simultaneously from a well shuffled pack of 52 playing cards. Find the probability distribution of the number of aces.
Two dice are thrown together and the number appearing on them noted. X denotes the sum of the two numbers. Assuming that all the 36 outcomes are equally likely, what is the probability distribution of X?
Find the probability distribution of the number of white balls drawn in a random draw of 3 balls without replacement, from a bag containing 4 white and 6 red balls
From a lot containing 25 items, 5 of which are defective, 4 are chosen at random. Let X be the number of defectives found. Obtain the probability distribution of X if the items are chosen without replacement .
Two cards are drawn simultaneously from a well-shuffled deck of 52 cards. Find the probability distribution of the number of successes, when getting a spade is considered a success.
A fair die is tossed twice. If the number appearing on the top is less than 3, it is a success. Find the probability distribution of number of successes.
Four balls are to be drawn without replacement from a box containing 8 red and 4 white balls. If X denotes the number of red balls drawn, then find the probability distribution of X.
Find the mean and standard deviation of each of the following probability distribution:
| xi : | 1 | 3 | 4 | 5 |
| pi: | 0.4 | 0.1 | 0.2 | 0.3 |
Find the mean and standard deviation of each of the following probability distribution :
| xi : | -5 | -4 | 1 | 2 |
| pi : | \[\frac{1}{4}\] | \[\frac{1}{8}\] | \[\frac{1}{2}\] | \[\frac{1}{8}\] |
Find the mean and standard deviation of each of the following probability distribution :
| xi : | -2 | -1 | 0 | 1 | 2 |
| pi : | 0.1 | 0.2 | 0.4 | 0.2 | 0.1 |
A discrete random variable X has the probability distribution given below:
| X: | 0.5 | 1 | 1.5 | 2 |
| P(X): | k | k2 | 2k2 | k |
Determine the mean of the distribution.
A fair die is tossed. Let X denote twice the number appearing. Find the probability distribution, mean and variance of X.
A die is tossed twice. A 'success' is getting an odd number on a toss. Find the variance of the number of successes.
Three cards are drawn at random (without replacement) from a well shuffled pack of 52 cards. Find the probability distribution of number of red cards. Hence, find the mean of the distribution .
An urn contains 5 red and 2 black balls. Two balls are randomly drawn, without replacement. Let X represent the number of black balls drawn. What are the possible values of X ? Is X a random variable ? If yes, then find the mean and variance of X.
For what value of k the following distribution is a probability distribution?
| X = xi : | 0 | 1 | 2 | 3 |
| P (X = xi) : | 2k4 | 3k2 − 5k3 | 2k − 3k2 | 3k − 1 |
Using the truth table verify that p ∨ (q ∧ r) ≡ (p ∨ q) ∧ (p ∨ r).
Verify the following function, which can be regarded as p.m.f. for the given values of X :
| X = x | -1 | 0 | 1 |
| P(x) | -0.2 | 1 | 0.2 |
Find expected value and variance of X, where X is number obtained on uppermost face when a fair die is thrown.
Solve the following :
Identify the random variable as either discrete or continuous in each of the following. Write down the range of it.
20 white rats are available for an experiment. Twelve rats are male. Scientist randomly selects 5 rats number of female rats selected on a specific day
Determine whether each of the following is a probability distribution. Give reasons for your answer.
| x | 0 | 1 | 2 | 3 | 4 |
| P(x) | 0.1 | 0.5 | 0.2 | –0.1 | 0.3 |
Determine whether each of the following is a probability distribution. Give reasons for your answer.
| x | 0 | 1 | 2 |
| P(x) | 0.1 | 0.6 | 0.3 |
Determine whether each of the following is a probability distribution. Give reasons for your answer.
| y | –1 | 0 | 1 |
| P(y) | 0.6 | 0.1 | 0.2 |
10 balls are marked with digits 0 to 9. If four balls are selected with replacement. What is the probability that none is marked 0?
Solve the following problem :
The probability that a component will survive a check test is 0.6. Find the probability that exactly 2 of the next 4 components tested survive.
Solve the following problem :
A computer installation has 3 terminals. The probability that any one terminal requires attention during a week is 0.1, independent of other terminals. Find the probabilities that 1 terminal requires attention during a week.
Find the probability distribution of the number of successes in two tosses of a die, where a success is defined as six appears on at least one die
Let a pair of dice be thrown and the random variable X be the sum of the numbers that appear on the two dice. Find the mean or expectation of X and variance of X
The probability distribution of a random variable x is given as under:
P(X = x) = `{{:("k"x^2, "for" x = 1"," 2"," 3),(2"k"x, "for" x = 4"," 5"," 6),(0, "otherwise"):}`
where k is a constant. Calculate E(X)
Find the probability distribution of the number of successes in two toves of a die where a success is define as:- Six appeared on at least one die.
Find the mean number of defective items in a sample of two items drawn one-by-one without replacement from an urn containing 6 items, which include 2 defective items. Assume that the items are identical in shape and size.
A random variable X has the following probability distribution:
| x | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| P(x) | k | 2k | 2k | 3k | k2 | 2k2 | 7k2 + k |
Find:
- k
- P(X < 3)
- P(X > 4)
A large chain retailer purchases an electric device from the manufacturer. The manufacturer indicates that the defective rate of the device is 10%. The inspector of the retailer randomly selects 4 items from a shipment. Complete the following activity to find the probability that the inspector finds at most one defective item in the 4 selected items.
Solution:
Here, n = 4
p = probability of defective device = 10% = `10/100 = square`
∴ q = 1 - p = 1 - 0.1 = `square`
X ∼ B(4, 0.1)
`P(X=x)=""^n"C"_x p^x q^(n-x)= ""^4"C"_x (0.1)^x (0.9)^(4 - x)`
P[At most one defective device] = P[X ≤ 1]
= P[X=0] + P[X=1]
= `square+square`
∴ P[X ≤ 1] = `square`
