Advertisements
Advertisements
Question
Calculate the magnetic dipole moment corresponding to the motion of the electron in the ground state of a hydrogen atom.
Solution
Mass of the electron, m = 9.1×10-31kg
Radius of the ground state, r = 0.53×10-10m
Let f be the frequency of revolution of the electron moving in ground state and A be the area of orbit.
Dipole moment of the electron (μ) is given by
μ = niA = qfA
`= e xx (me^4)/(4∈_0^2h^3n^3)xx(pi^2n^2)`
`= (me^5xx (pir^2n^2))/(4∈_0^2h^3n^3)`
Here,
h = Planck's constant
e = Charge on the electron
`epsilon_0` = Permittivity of free space
n = Principal quantum number
`therefore mu = ((9.1xx10^-13)(1.6xx10^-19)^5xxpi xx(0.53xx10^-10)^2)/(4 xx (8.85xx10^-12)^2xx(6.64xx10^-34)^3xx(1)^3`
= 0.000917 × 10-20
= 9.176 × 10-24 A-m25
APPEARS IN
RELATED QUESTIONS
Obtain an expression for the radius of Bohr orbit for H-atom.
(i) State Bohr's quantization condition for defining stationary orbits. How does the de Broglie hypothesis explain the stationary orbits?
(ii) Find the relation between three wavelengths λ1, λ2 and λ3 from the energy-level diagram shown below.
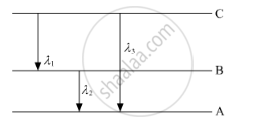
What is the maximum number of emission lines when the excited electron of an H atom in n = 6 drops to the ground state?
Using Bohr’s postulates, obtain the expressions for (i) kinetic energy and (ii) potential energy of the electron in stationary state of hydrogen atom.
Draw the energy level diagram showing how the transitions between energy levels result in the appearance of Lymann Series.
Using Bohr’s postulates for hydrogen atom, show that the total energy (E) of the electron in the stationary states tan be expressed as the sum of kinetic energy (K) and potential energy (U), where K = −2U. Hence deduce the expression for the total energy in the nth energy level of hydrogen atom.
The Bohr radius is given by `a_0 = (∈_0h^2)/{pime^2}`. Verify that the RHS has dimensions of length.
A beam of light having wavelengths distributed uniformly between 450 nm to 550 nm passes through a sample of hydrogen gas. Which wavelength will have the least intensity in the transmitted beam?
When a photon is emitted by a hydrogen atom, the photon carries a momentum with it. (a) Calculate the momentum carries by the photon when a hydrogen atom emits light of wavelength 656.3 nm. (b) With what speed does the atom recoil during this transition? Take the mass of the hydrogen atom = 1.67 × 10−27 kg. (c) Find the kinetic energy of recoil of the atom.
Obtain Bohr’s quantisation condition for angular momentum of electron orbiting in nth orbit in hydrogen atom on the basis of the wave picture of an electron using de Broglie hypothesis.
In which of the following systems will the wavelength corresponding to n = 2 to n = 1 be minimum?
If l3 and l2 represent angular momenta of an orbiting electron in III and II Bohr orbits respectively, then l3: l2 is :
How are various lines of Lyman series formed? Explain on the basis of Bohr’s theory.
What is the energy in joules released when an electron moves from n = 2 to n = 1 level in a hydrogen atom?
In Bohr model of hydrogen atom, which of the following is quantised?
Consider two different hydrogen atoms. The electron in each atom is in an excited state. Is it possible for the electrons to have different energies but same orbital angular momentum according to the Bohr model? Justify your answer.
The ratio of the ionization energy of H and Be+3 is ______.
The number of times larger the spacing between the energy levels with n = 3 and n = 8 spacing between the energy level with n = 8 and n = 9 for the hydrogen atom is ______.
The energy of an electron in the first Bohr orbit of the H-atom is −13.6 eV. The energy value of an electron in the excited state of Li2+ is ______.
What is the energy associated with first orbit of Li2+ (RH = 2.18 × 10-18)?
