Advertisements
Advertisements
Question
Construct a Δ ABC with BC = 6.5 cm, AB = 5.5 cm, AC = 5 cm. Construct the incircle of the triangle. Measure and record the radius of the incircle.
Solution
BC = 6.5 cm, AB = 5.5 cm, AC = 5 cm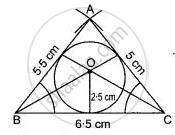
Radius of the circle = 2.5 cm
APPEARS IN
RELATED QUESTIONS
Use ruler and compasses only for the following questions. All constructions lines and arcs must be clearly shown
Construct a ABC in which BC = 6.5 cm, ABC = 60°, AB = 5 cm.
Using ruler and compass only, construct a ΔABC such that BC = 5 cm and AB = 6.5
cm and ∠ABC = 120°
1) Construct a circum-circle of ΔABC
2) Construct a cyclic quadrilateral ABCD, such that D is equidistant from AB and BC.
Using ruler and compasses only, draw an equilateral triangle of side 5 cm. Draw its inscribed circle. Measure the radius of the circle.
Construct a regular hexagon of side 4 cm. Construct a circle circumscribing the hexagon.
Contruct a ΔABC with BC = 6.5 cm, AB = 5.5 cm, AC = 5 cm. Construct the incircle of the triangle. Measure and record the radius of the incricle.
Draw a circle of radius 2. 5 cm and circumscribe a square about it.
Perpendicular bisectors of the sides AB and AC of a triangle ABC meet at O.
Does the perpendicular bisector of BC pass through O?
In triangle ABC, ∠ABC = 90°, AB = 6 cm, BC = 7.2 cm and BD is perpendicular to side AC. Draw circumcircle of triangle BDC and then state the length of the radius of this circumcircle drawn.
Construct an isosceles triangle ABC such that AB = 6 cm, BC = AC = 4 cm. Bisect ∠C internally and mark a point P on this bisector such that CP = 5 cm. Find the points Q and R which are 5 cm from P and also 5 cm from the line AB.
Ruler and compasses only may be used in this question. All constructions lines and arcs must be clearly shown, and the be sufficient length and clarity to permit assessment:
(i) Construct a triangle ABC, in which AB = 9 cm, BC = 10 cm and angle ABC = 45°.
(ii) Draw a circle, with center A and radius 2.5 cm. Let it meet AB at D.
(iii) Construct a circle to touch the circle with center A externally at D and also to touch the line BC.
