Advertisements
Advertisements
Question
Use ruler and compasses only for this question:
(i) Construct A ABC, where AB = 3.5 cm, BC = 6 cm and ∠ ABC = 60°.
(ii) Construct the locus of points inside the triangle which are equidistant from BA and BC.
(iii) Construct the locus of points inside the triangle which are equidistant from B and C.
(iv) Mark the point P which is equidistant from AB, BC, and also equidistant from B and C. Measure and record the length of PB.
Solution
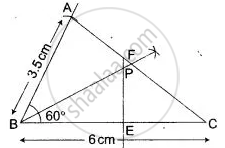
(i) See Figure,
(ii) Inside the triangle point, P is equidistant from BA and BC.
(iii) Line EF is the locus of points inside the triangle which are equidistant from B and C.
(iv) PB = 3.5 cm.
APPEARS IN
RELATED QUESTIONS
Using a ruler and compasses only:
1) Construct a triangle ABC with the following data: AB = 3.5 cm, BC = 6 cm and ABC = 120°
2) In the same diagram, draw a circle with BC as diameter. Find a point P on the circumference of the circle which is equidistant from AB and BC.
3) Measure ∠BCP.
Perpendicular bisectors of the sides AB and AC of a triangle ABC meet at O.
- What do you call the point O?
- What is the relation between the distances OA, OB and OC?
- Does the perpendicular bisector of BC pass through O?
Constuct a triangle ABC with AB = 5.5 cm, AC = 6 cm and ∠BAC = 105°. Hence:
- Construct the locus of point equdistant from BA and BC.
- Construct the locus of points equidistant from B and C.
- Mark the point which satisfies the above two loci as P. Measure and write the length of PC.
Construct Δ ABC in which AB = 5 cm, BC = 4. 5 cm and ∠ ABC = 60" .. Construct a cirde to circumscribe. Δ ABC.
Draw line segments OA = 4.5 cm, OB = 3.2 cm such that ∠ AOB = 45°. Construct a circle touching OA at A and passing through B.
Perpendicular bisectors of the sides AB and AC of a triangle ABC meet at O.
What is the relation between the distances OA, OB and OC?
In triangle ABC, ∠ABC = 90°, AB = 6 cm, BC = 7.2 cm and BD is perpendicular to side AC. Draw circumcircle of triangle BDC and then state the length of the radius of this circumcircle drawn.
Construct an isosceles triangle ABC such that AB = 6 cm, BC = AC = 4 cm. Bisect ∠C internally and mark a point P on this bisector such that CP = 5 cm. Find the points Q and R which are 5 cm from P and also 5 cm from the line AB.
Construct a Δ ABC with BC = 6.5 cm, AB = 5.5 cm, AC = 5 cm. Construct the incircle of the triangle. Measure and record the radius of the incircle.
Construct a ΔABC with base BC = 3.5 cm, vertical angle ∠ BAC = 45°, and median through the vertex A is 3.5 cm. Write also the steps of construction.
