Advertisements
Advertisements
Question
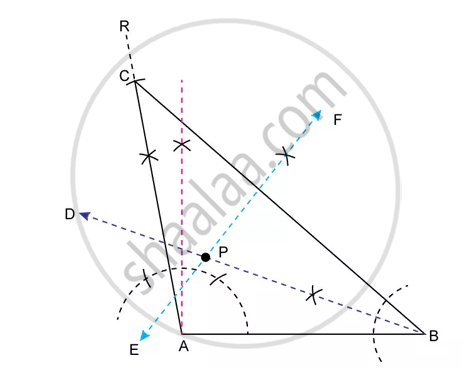
Constuct a triangle ABC with AB = 5.5 cm, AC = 6 cm and ∠BAC = 105°. Hence:
- Construct the locus of point equdistant from BA and BC.
- Construct the locus of points equidistant from B and C.
- Mark the point which satisfies the above two loci as P. Measure and write the length of PC.
Solution
Steps of construction:
- Draw AB = 5.5 cm.
- Construct ∠BAR = 105°.
- With centre A and radius 6 cm, cut off arc on AR at C.
- Join BC. ABC is the required triangle.
- Draw angle bisector BD of ∠ABC, which is the locus of points equidistant from BA and BC.
- Draw perpendicular bisector EF of BC, which is the loucs of point equidistant from B and C.
- BD and EF intersect each other at point P. Thus, P satisfies the above two loci. By measurement, PC = 4.8 cm.
APPEARS IN
RELATED QUESTIONS
Construct a regular hexagon of side 5 cm. Hence construct all its lines of symmetry and name them.
Construct a triangle ABC in which base BC = 6 cm, AB = 5.5 cm and ∠ABC = 120°.
Construct a circle circumscribing the triangle ABC.
Draw a cyclic quadrilateral ABCD so that D is equidistant from B and C.
Construct a regular hexagon of side 4 cm. Construct a circle circumscribing the hexagon.
Using a ruler and compasses only:
- Construct a triangle ABC with the following data: AB = 3.5 cm, BC = 6 cm and ∠ABC = 120°.
- In the same diagram, draw a circle with BC as diameter. Find a point P on the circumference of the circle which is equidistant from AB and BC.
- Measure ∠BCP.
Contruct a ΔABC with BC = 6.5 cm, AB = 5.5 cm, AC = 5 cm. Construct the incircle of the triangle. Measure and record the radius of the incricle.
In triangle ABC, ∠ABC = 90°, AB = 6 cm, BC = 7.2 cm and BD is perpendicular to side AC. Draw circumcircle of triangle BDC and then state the length of the radius of this circumcircle drawn.
Construct a triangle ABC, given that the radius of the circumcircle of triangle ABC is 3.5 cm, ∠ BCA = 45° and ∠ BAC = 60°.
Using ruler and compass only, construct a triangle ABC such that AB = 5 cm, ABC = 75°, and the radius of the circumcircle of triangle ABC is 3.5 cm. On the same diagram, construct a circle, touching AB at its middle point and also touching the side AC.
Construct a triangle whose sides are 4.4 cm, 5.2 cm, and 7.1 cm. Construct its circumcircle. Write also the steps of construction.
Construct a Δ ABC with BC = 6.5 cm, AB = 5.5 cm, AC = 5 cm. Construct the incircle of the triangle. Measure and record the radius of the incircle.
