Advertisements
Advertisements
Question
Derive an expression for phase angle between the applied voltage and current in a series RLC circuit.
Solution
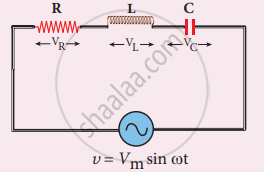
AC circuit containing R, L and C
L(VL) leads I by `π/2` and voltage across C(VC) lags I by `π/2`
Phasor diagram is drawn with the current.
The length of these phasors are
OI = Im, OA = ImR, OB = ImχL;
OC = ImχC
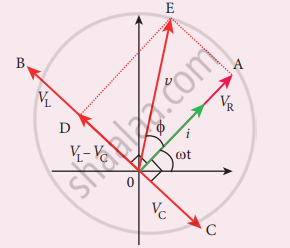
Phasor diagram for a series RLC – circuit when VL > VC
Vm2 = VR2 + (VL – VC)2
`= sqrt(("I"_"m""R")^2 + ("I"_"m""X"_"L" - "I"_"m""X"_"C")^2)`
`= "I"_"m" sqrt("R"^2 + ("X"_"L" - "X"_"C")^2)` or `"I"_"m" = "V"_"m"/"Z"`
where Z = `sqrt("R"^2 + ("X"_"L" - "X"_"C")^2)` It is impedence of circuit.
From phasor diagram, phase angle between angle between v and i is
`tan phi = ("V"_"L" - "V"_"L")/"V"_"R" = ("X"_"L" - "X"_"C")/"R"`
Special cases:
i) If χL> χC, (χL – χC) is positive and Φ is also positive.
∴ υ = Vmsin ωt; i = Im(sin(ωt – Φ))
ii) if χL < χC, (χL – χC) is negative and Φ is negative.
∴ υ = Vmsin ωt; i = Im(sin(wt + Φ))
APPEARS IN
RELATED QUESTIONS
Define electric resonance.
What do you mean by resonant frequency?
Calculate the instantaneous value at 60°, average value and RMS value of an alternating current whose peak value is 20 A.
In any ac circuit, is the applied instantaneous voltage equal to the algebraic sum of the instantaneous voltages across the series elements of the circuit? Is the same true for rms voltage?
A choke coil in series with a lamp is connected to a dc line. The lamp is seen to shine brightly. Insertion of an iron core in the choke causes no change in the lamp’s brightness. Predict the corresponding observations if the connection is to an ac line.
An alternating voltage source of variable angular frequency ‘w’ and fixed amplitude ‘V’ is connected in series with a capacitance C and electric bulb of resistance R(inductance zero). When ‘w’ is increased ______.
In an a.c circuit, peak value of voltage is 423 volts, its effective voltage is ______.
An inductor of 0.5 mH, a capacitor of 200 µF, and a resistor of 2Ω are connected in series with a 220V ac source. If the current is in phase with the emf, the frequency of ac source will be ______ × 102 Hz.
An alternating current I = 14 sin (100 πt) A passes through a series combination of a resistor of 30 Ω and an inductor of `(2/(5pi))` H. Taking `sqrt2` = 1.4 calculate the rms value of the voltage drops across the resistor and the inductor.
Draw graphs showing the variations of inductive reactance and capacitive reactance with the frequency of the applied ac source.
