Advertisements
Advertisements
Question
Derive th e equation of motion.
S = ut+ `1/2` at2,
Where the symbols have their usual meanings
Solution
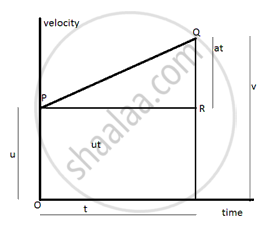
In figure we know
S = area of trapezium OSQP
Area of trapezium OSQP = 1/2 (sum of parallel sides) x perpendicular distance between them.
S = 1/2 (OP + SQ) x PR.
PR= QR/a= (QS-RS) / a
PR= (v - u)/a = t
So PR= t .
Substituting these values in expression of area of trapezium we get
S= 1/2 (u + v) xt
S = 1/2 (u +v) x (u - v)/a.
2aS = v2 - u2
v2 - u2 = 2 as.
This is known as third equation of motion.
APPEARS IN
RELATED QUESTIONS
Name the physical quantity which gives us an idea of how slow or fast a body is moving.
Write the formula for acceleration. Give the meaning of each symbol which occurs in it.
If a sprinter runs a distance of 100 metres in 9.83 seconds, calculate his average speed in km/h.
A motorcyclist starts from rest and reaches a speed of 6 m/s after travelling with uniform acceleration for 3 s. What is his acceleration ?
A train starting from rest moves with a uniform acceleration of 0.2 m/s2 for 5 minutes. Calculate the speed acquired and the distance travelled in this time.
Express 15 m s-1 in km h-1.
For the motion with uniform velocity , how is the distance travelled related to the time ?
Figure shows the displacement of a body at different times .

Calculate the average velocity during the time interval 5 s to 9 s ,
[Hint : From 5 s to 9 s , displacement = 7 m - 3m = 4m]
From the displacement-time graph of a cyclist given below in the Figure, find The average velocity in the first 4 s.

How many variables are present in each equation of motion?
