Advertisements
Advertisements
Question
Derive the equation for effective focal length for lenses in contact.
Solution
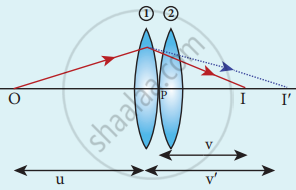
Lenses in contact
- Two lenses (1) and (2) having focal length are placed coaxially in contact.
- Lens equation for first equation be
`1/"v'" - 1/"u" = 1/"f"_1` - Lens equation for the second lens be
`1/"v" − 1/"v′" = 1/"f"_2` - Adding the above equation
`1/"v" - 1/"u" = 1/"f"_1 + 1/"f"_2` - If the combinations acts as single lens then,
`1/"v" - 1/"u" = 1/"f"` - On comparing,
`1/"F" = 1/"f"_1 + 1/"f"_2`
∴ For any number of lens in contact
`1/"f"_1 + 1/"f"_2 + 1/"f"_3 + ....`
APPEARS IN
RELATED QUESTIONS
An object is placed in front of a convex mirror of focal length of f and the maximum and minimum distance of an object from the mirror such that the image formed is real and magnified.
What are primary focus and secondary focus of convex lens?
Arrive at lens equation from lens maker’s formula.
Obtain the equation for lateral magnification for thin lens.
What is power of a lens?
Derive the equation for thin lens and obtain its magnification.
Derive the equation for effective focal length for lenses in out of contact.
A thin converging glass lens made of glass with refractive index 1.5 has a power of + 5.0 D. When this lens is immersed in a liquid of refractive index n, it acts as a divergent lens of focal length 100 cm. What must be the value of n?
If the distance D between an object and screen is greater than 4 times the focal length of a convex lens, then there are two positions of the lens for which images are formed on the screen. This method is called conjugate foci method. If d is the distance between the two positions of the lens, obtain the equation for a focal length of the convex lens.
A point object is placed at 20 cm from a thin plano-convex lens of focal length 15 cm whose plane surface is silvered. Locate the position and nature of the final image.
