Question

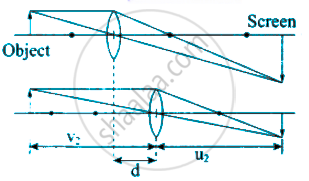
If the distance D between an object and screen is greater than 4 times the focal length of a convex lens, then there are two positions of the lens for which images are formed on the screen. This method is called conjugate foci method. If d is the distance between the two positions of the lens, obtain the equation for a focal length of the convex lens.

Answer 1

Let us fix the position of the object and place the screen to get the enlarged image first. Also, let us fix the position of the screen where we get the enlarged image.

Let D be the distance between object and screen. Let us mark the position of lens dv Then let us move the lens away from the object to get a diminished image. Let this position of lens be d₂. Let d be the distance between the lens position d₁ and d₂. Let V be the distance b/w image and lens. Let ‘u’ be the distance between object and lens.

From mirror equation,

`1/"v" + 1/"u" = 1/"f"`

Let us replace v by substituting v = D – u

`1/("D - u") + 1/"u" = 1/"f"`

we get the equation, u² -Du + fD = 0

the quadratic equation for above equation,

u = `("D" +- sqrt("D"^2 - 4"fD"))/2`

When D = 4f, we get the only the position of the lens to get an image.
This corresponds to placing the object at 2f and getting the image at 2f on the other side. Hence, for the displacement method, we need D > 4 f. When this condition is satisfied we get

u₁ = `("D" - sqrt("D"^2 - 4"fD"))/2`; corresponding v₁ – D – u₂ = `("D" + sqrt("D"^2 - 4"fD"))/2`  after changing the location

u₁ = `("D" + sqrt("D"^2 - 4"fD"))/2`; corresponding v₂ – D – u₂ = `("D" - sqrt("D"^2 - 4"fD"))/2` now the displacement d = v₁ – u₁ = u₁ – v₁ = `sqrt("D"^2 - 4"fD")`

Hence we get focal length, ƒ = `("D"^2 - "d"^2)/"4D"`