Advertisements
Advertisements
Question
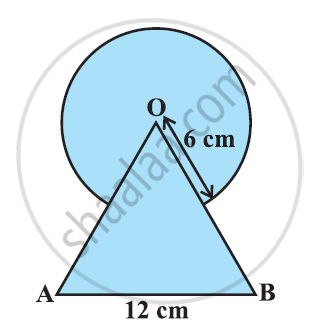
दी गई आकृति में, छायांकित भाग का क्षेत्रफल ज्ञात कीजिए, जहाँ भुजा 12 सेमी वाले एक समबाहु त्रिभुज OAB के शीर्ष O को केंद्र मान कर 6 सेमी त्रिज्या वाला एक वृत्तीय चाप खींचा गया है। [उपयोग Π = `22/7`]
Solution
हम जानते हैं कि एक समबाहु त्रिभुज का प्रत्येक अंतः कोण 60° का होता है।
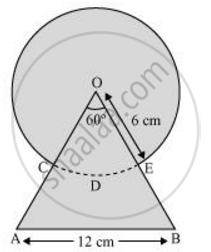
त्रिज्यखंड OCDE का क्षेत्रफल = `60^@/360^@pir^2`
`=1/6xx22/7xx6xx6`
`= 132/7 "सेमी"^2`
त्रिभुजOAB का क्षेत्रफल = `sqrt3/4(12)^2 = (sqrt3xx12xx12)/4 = 36sqrt3 cm^2`
वृत्त का क्षेत्रफल = `pir^2 = 22/7xx6xx6 = 792/7 "सेमी"^2`
छायांकित क्षेत्र का क्षेत्रफल = OAB का क्षेत्रफल + वृत्त का क्षेत्रफल - त्रिज्यखंड OCDE का क्षेत्रफल
`= 36sqrt3 + 792/7 - 132/7`
`=(36sqrt3 + 660/7) "सेमी"^2`
APPEARS IN
RELATED QUESTIONS
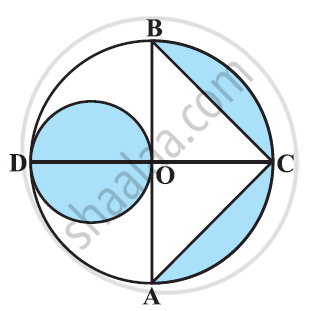
दी गई आकृति में AB और CD केंद्र O वाले एक वृत्त के दो परस्पर लंब व्यास हैं तथा OD छोटे वृत्त का व्यास है। यदि OA = 7 सेमी है, तो छायांकित भाग का क्षेत्रफल ज्ञात कीजिए। [उपयोग Π = `22/7`]
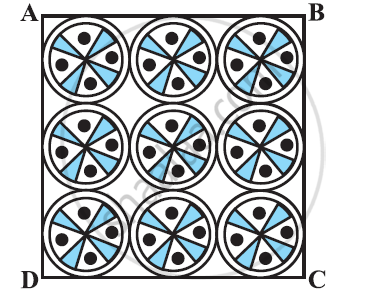
एक वर्गाकार रूमाल पर, नौ वृत्ताकार डिजाइन बने हैं, जिनमें से प्रत्येक की त्रिज्या 7 सेमी है। रूमाल के शेष भाग का क्षेत्रफल ज्ञात कीजिए।
दी गई आकृति में OACB केंद्र O और त्रिज्या 3.5 सेमी वाले एक वृत्त का चतुर्थांस है। यदि OD = 2 सेमी है, तो निम्नलिखित के क्षेत्रफल ज्ञात कीजिए:
- चतुर्थांस OACB
- छायांकित भाग
[उपयोग Π = `22/7`]

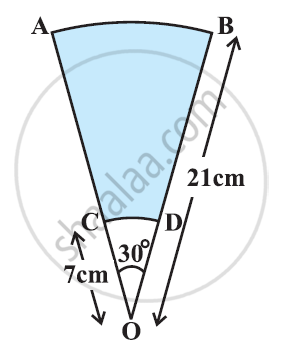
AB और CD केंद्र O तथा त्रिज्याओं 21 सेमी और 7 सेमी वाले दो सकेंद्रीय वृत्तों के क्रमश: दो चाप हैं। यदि ∠AOB = 30° तो छायांकित भाग का क्षेत्रफल ज्ञात कीजिए।
[उपयोग Π = `22/7`]
दी गई आकृति में, ABC त्रिज्या 12 सेमी वाले एक वृत का चतुर्थांश है तथा BC को व्यास मानकर एक अर्धवृत्त्त खींचा गया है। छायांकित भाग का क्षेत्रफल ज्ञात कीजिए। [उपयोग Π = 22/7]

दी गई आकृति में छायांकित डिजाइन का क्षेत्रफल ज्ञात कीजिए, जो 8 सेमी त्रिज्याओं वाले दो वृत्तों के चतुर्थांशों के बीच उभयनिष्ठ है। [उपयोग Π = 22/7]

त्रिज्या 8 cm वाले एक वृत्त के अंतर्गत खींचे जा सकने वाले वर्ग का क्षेत्रफल ______ है।
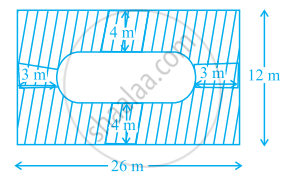
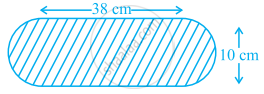
आकृति में दर्शायी गयी फूलों की क्यारी (अर्धवृत्ताकार सिरों वाली) का क्षेत्रफल ज्ञात कीजिए।
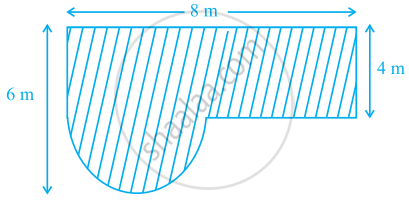
आकृति में दर्शाये गये छायांकित खेत का क्षेत्रफल ज्ञात कीजिए।
आकुति में, छायांकित क्षेत्र का क्षेत्रफल ज्ञात कीजिए।